题目内容
已知:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点M、N分别在边AO和边OD上,且AM= AO,ON=
AO,ON= OD,设
OD,设 =
= ,
, =
= ,试用
,试用 、
、 的线性组合表示向量
的线性组合表示向量 和向量
和向量 .
.
【答案】分析:根据平行四边形法则求出 ,再根据平行四边形的对角线互相平分表示
,再根据平行四边形的对角线互相平分表示 ,然后根据OM=
,然后根据OM= AO,再表示出
AO,再表示出 即可;
即可;
根据平行线分线段成比例定理求出MN∥AD,并求出 =
= ,然后根据向量的表示
,然后根据向量的表示 =
=
 即可得解.
即可得解.
解答:解:根据平行四边形法则, =
= +
+ =
= +
+ ,
,
∵平行四边形ABCD,
∴AO= AC,
AC,
∴ =
=
 =
= (
( +
+ ),
),
∵AM= AO,
AO,
∴OM= AO,
AO,
∴ =-
=-
 ,
,
∴ =-
=- ×
× (
( +
+ )=-
)=-
 -
-
 ;
;
∵AM= AO,ON=
AO,ON= OD,
OD,
∴ =
= =
= ,
,
∴MN∥AD,
∴ =
= =
= ,
,
∴ =
=
 ,
,
又∵平行四边形ABCD,
∴ =
= =
= ,
,
∴ =
=
 .
.
点评:本题是对向量的考查,主要利用了平行四边形法则,平行四边形的对角线互相平分的性质,平行线分线段成比例定理,要注意线性组合的特点的利用.
 ,再根据平行四边形的对角线互相平分表示
,再根据平行四边形的对角线互相平分表示 ,然后根据OM=
,然后根据OM= AO,再表示出
AO,再表示出 即可;
即可;根据平行线分线段成比例定理求出MN∥AD,并求出
 =
= ,然后根据向量的表示
,然后根据向量的表示 =
=
 即可得解.
即可得解.解答:解:根据平行四边形法则,
 =
= +
+ =
= +
+ ,
,∵平行四边形ABCD,
∴AO=
 AC,
AC,∴
 =
=
 =
= (
( +
+ ),
),∵AM=
 AO,
AO,∴OM=
 AO,
AO,∴
 =-
=-
 ,
,∴
 =-
=- ×
× (
( +
+ )=-
)=-
 -
-
 ;
;∵AM=
 AO,ON=
AO,ON= OD,
OD,∴
 =
= =
= ,
,∴MN∥AD,
∴
 =
= =
= ,
,∴
 =
=
 ,
,又∵平行四边形ABCD,
∴
 =
= =
= ,
,∴
 =
=
 .
.点评:本题是对向量的考查,主要利用了平行四边形法则,平行四边形的对角线互相平分的性质,平行线分线段成比例定理,要注意线性组合的特点的利用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
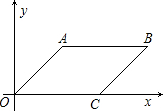 如图,在平行四边形ABC0中,已知点A、C两点的坐标为A(
如图,在平行四边形ABC0中,已知点A、C两点的坐标为A(
 (2013•南平模拟)如图,已知四边形ABCD.请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予证明.
(2013•南平模拟)如图,已知四边形ABCD.请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予证明. 如图,在平行四边形OABC中,已知点A、C两点的坐标为A (
如图,在平行四边形OABC中,已知点A、C两点的坐标为A (