题目内容
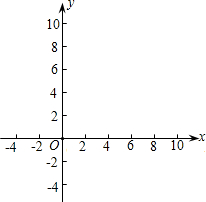 在△ABC中,设BC=x,BC上的高为y,△ABC的面积等于4.?
在△ABC中,设BC=x,BC上的高为y,△ABC的面积等于4.?(1)写出y和x之间的函数关系式,并指出自变量x的取值范围;然后作出它的函数图象;
(2)当△ABC为等腰直角三角形时,求出图象上对应点D、E的坐标;?
(3)求△DOE的面积.
分析:(1)由题意,BC=x,BC上的高为y,△ABC的面积等于4,可知xy=2×4,即y=
;
(2)由于未给出哪个是直角,需分情况讨论,再利用两函数组成的方程组即可得交点坐标.
(3)要求三角形的面积可利用反比例函数系数k的几何意义,分别过D、E作DM垂直x轴于M,EN垂直x轴于N,转化为可知的面积求解.
| 8 |
| x |
(2)由于未给出哪个是直角,需分情况讨论,再利用两函数组成的方程组即可得交点坐标.
(3)要求三角形的面积可利用反比例函数系数k的几何意义,分别过D、E作DM垂直x轴于M,EN垂直x轴于N,转化为可知的面积求解.
解答: 解:(1)y=
解:(1)y=
,图象(略)
(2)①当∠A=90°时,即
解得
即对应点D的坐标为(4,2)
②当∠B=90°时,即
,
解得
,即对应点E的坐标为(2
,2
)
(3)分别过D、E作DM垂直x轴于M,EN垂直x轴于N,
S△DOE=S△EON+S梯形DENM-S△DOM
=
×2
×2
+
×(2+2
)(4-2
)-
×4×2.
 解:(1)y=
解:(1)y=| 8 |
| x |
(2)①当∠A=90°时,即
|
解得
|
②当∠B=90°时,即
|
解得
|
| 2 |
| 2 |
(3)分别过D、E作DM垂直x轴于M,EN垂直x轴于N,
S△DOE=S△EON+S梯形DENM-S△DOM
=
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查反比例函数k的几何意义的灵活运用,出题角度新颖,是道不错的题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
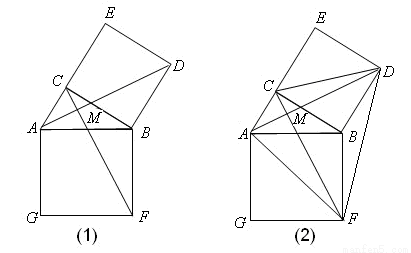
 (2013•河池)如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.
(2013•河池)如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.