题目内容

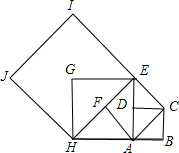如图设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，此时正方形AEGH的边长为
 
，如此下去，则第n个正方形的边长为
 
．
考点：正方形的性质
专题：规律型
分析：根据正方形的对角线等于边长的
2
倍依次求解，再根据指数的变化规律求出第n个正方形的边长．
解答：解：∵正方形ABCD的边长为1，
∴第2个正方形ACEF的边长AC=
2
，
第3个正方形AEGH的边长AE=
2
AC=（
2
）2=2，
…，
第n个正方形的边长=（
2
）n-1．
故答案为：2；（
2
）n-1．
点评：本题考查了正方形的性质，图形的变化规律，主要利用了正方形的对角线等于边长的
2
倍，需熟记．
练习册系列答案
相关题目
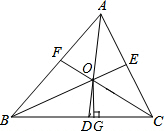如图，△ABC中，三条内角平分线AD、BE、CF相交于点O，OG⊥BC于点G．
（1）若∠ABC=40°，∠BAC=60°，求∠BOD和∠COG的度数．
（2）若∠ABC=α，∠BAC=β，则∠BOD和∠COG相等吗？请说明理由．
海宝在研究数学问题时发现了一个有趣的现象：

（1）任选两组符合条件a+b=ab的正数a，b的值；
（2）选（1）中两组a，b值中的一组值，验证海宝的结论：
b
a
+
a
b
比ab小2；
（3）在一般情形下，验证海宝的结论．
计算：（3
2
-
12
）（
18
+2
3
）
方程2x+y=5的一个解
x=2
y=(      )
 
．
若x+
1
x
=
10
，则x-
1
x
=
 
．
如图1是长方形纸袋，将纸袋沿EF折叠成图2，再沿BF折叠成图3，若∠DEF=α，用α表示图3中∠CFE的大小为
 
．
如果x-y=5且y-z=5，那么z-x的值是
 
．
已知1.53=3.375，则
3-3375000
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网