Question

双曲线y=

1

x

（x＞0）与直线y=x在坐标系中的图象如图所示，点A、B在直线上AC、BD分别平行y轴，交曲线于C、D两点，若BD=2AC  则4OC²-OD²的值为

6

．

Answer 1

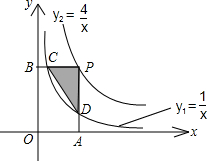
分析：根据A，B两点在直线y=x上，分别设A，B两点的坐标为（a，a），（b，b），得到点C的坐标为（a，

1

a

），点D的坐标为（b，

1

b

），线段AC=a-

1

a

，线段BD=b-

1

b

，根据BD=2AC，有b-

1

b

=2（a-

1

a

），然后利用勾股定理进行计算求出4OC²-OD²的值．

解答：解：设A（a，a），B（b，b），则C（a，

1

a

），D（b，

1

b

），
AC=a-

1

a

，BD=b-

1

b

，
∵BD=2AC，
∴b-

1

b

=2（a-

1

a

），
4OC²-OD²
=4（a²+

1

a2

）-（b²+

1

b2

）
=4[(a-

1

a

)2+2]-[(b-

1

b

)2+2]
=4(a-

1

a

)2+8-4(a-

1

a

)2-2
=6．
故答案为：6．

点评：本题考查的是反比例函数综合题，根据直线与反比例函数的解析式，设出点A，B的坐标后可以得到点C，D的坐标，运用勾股定理进行计算求出代数式的值．