题目内容
两条直线被第三条直线所截，同位角相等。（___）
×
【解析】试题分析：两条平行线被第三条直线所截，同位角相等．故本题答案为“×”．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
如图，△ABC和△A′B′C′关于直线l对称，下列结论中：
①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；
③l垂直平分CC′；
④直线BC和B′C′的交点不一定在l上，
正确的有（ ）
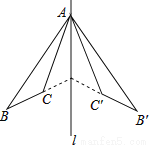
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称，
∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC正确；
③l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误．
综上所述，结论正确的是①②③共3个．
故... 观察图中的汽车商标，其中是轴对称图形的个数为
A、2 B、3 C、4 D、5
B
【解析】
试题分析：轴对称图形的定义：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
由图可得轴对称图形为第一个、第二个、第四个，故选B. 已知：如图，∠1=35º，AB⊥CD，垂足为O，EF经过点O。求∠2、∠3、∠4的度数。
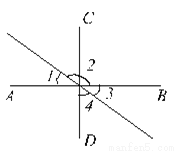
∠2=145°，∠3=35°， ∠4=55°
【解析】试题分析：首先根据对顶角的性质得出∠3的度数，根据邻补角的性质求出∠2的度数，最后根据垂直的定义求出∠4的度数．
试题解析：∵∠1和∠3是对顶角， ∴∠3=∠1=35°， ∵∠1+∠2=180°，
∴∠2=180°-∠1=180°-35°=145°， ∵AB⊥CD， ∴∠3+∠4=90°，
∴∠4=90°-∠3=90°-... 如果a,b,c为同一平面内的3条不同直线，若直线a⊥b，b⊥c，那么a∥c. （___）
√
【解析】试题分析：在同一平面内，垂直与同一条直线的两直线平行，故本题答案为“√”． 已知函数y=
x3+2，不画图象，解答下列问题：
（1）判断A（0，2）、B（2，0）、C（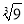
， ﹣1）三点是否在该函数图象上，说明理由；
（2）若点P（a，0）、Q（﹣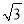
， b）都在该函数的图象上，试求a、b的值．
(1) B，C点不在该函数图象上，A点在该函数图象上；(2) a=,b=
【解析】试题分析：（1）分别将A，B，C点代入函数关系式进而判断即可；（2）分别将P，Q点代入函数关系式进而得出答案．
试题解析：
（1）当x=0时，y=2，
当x=2时，y=+2=，
当x=时，y=5，
故B，C点不在该函数图象上，A点在该函数图象上；
（2）当y=0时，0=x3+... 河道的剩水量Q（米3）和水泵抽水时间t（时）的关系图象如图，则水泵抽水前，河道内有______ 米3的水，水泵最多抽________ 小时，水泵抽8小时后，河道剩水量是________ 米3 ．
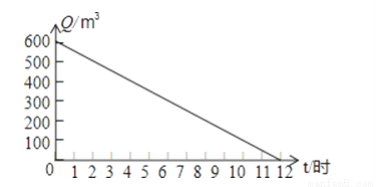
600 12 200
【解析】观察图象可知, 水泵抽水前，河道内有600米3的水，水泵最多抽12小时，水泵抽8小时后，河道剩水量是600－600÷12×8＝200米3． 如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，该桥的坡角∠ABC为15°，则该桥的水平距离BC的长是___米(精确到0.1米)．
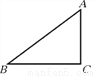
11.2
【解析】试题解析：Rt△ABC中,
(米).
故答案为：11.2. 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________．
37cm
【解析】①7cm是腰长时，三角形的三边分别为7cm、7cm、15cm，
∵7+7=14<15，
∴不能组成三角形，
②7cm是底边时，三角形的三边分别为7cm、15cm、15cm，
能组成三角形，
周长=7+15+15=37cm，
综上所述，它的周长是37cm.
故答案为：37cm.