题目内容
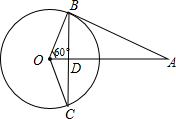
如图，已知⊙O的弦CD垂直于直径AB，点E在CD上，且EC = EB ．
（1）求证：△CEB∽△CBD ；
（2）若CE = 3，CB=5 ，求DE的长．
（1）证明见解析；（2）
【解析】
试题分析：（1）根据有两组角对应相等的两个三角形相似来判定其相似；
（2）根据相似三角形的对应边成比例先求出CD的长，已知CE的长，那么DE的长就容易求得了．
试题解析：（1）证明：∵弦CD垂直于直径AB，
∴BC=BD．
∴∠C=∠D．
又∵EC=EB，
∴∠C=∠CBE．
∴∠D=∠CBE．
又∵∠C=∠C，
∴△CEB∽△CBD．
（2）∵△CEB∽△CBD，
∴
∴CD=
∴DE=CD-CE=
考点：1．相似三角形的判定与性质；2．圆周角定理．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
