题目内容
 如图.在△ABC中,∠ABC=∠ACB,AC=8cm,BC=4cm,DE是AC的垂直平分线交AB于点D,交AC于点E,则△BDC的周长为( )
如图.在△ABC中,∠ABC=∠ACB,AC=8cm,BC=4cm,DE是AC的垂直平分线交AB于点D,交AC于点E,则△BDC的周长为( )| A、10cm | B、17cm |
| C、11cm | D、12cm |
考点:线段垂直平分线的性质
专题:
分析:根据在△ABC中,∠ABC=∠ACB得出AB=AC,再由线段垂直平分线的性质求出AD=CD,求出△BDC的周长是AB+BC,代入求出即可.
解答:解:∵在△ABC中,∠ABC=∠ACB,
∴AB=AC=8cm,
∵DE是AC的垂直平分线,
∴AD=CD,
∵AB=AC=8cm,BC=4cm,
∴△BDC的周长是:CD+BD+BC=AD+BD+BC=AB+BC=8+4=12(cm).
故选D.
∴AB=AC=8cm,
∵DE是AC的垂直平分线,
∴AD=CD,
∵AB=AC=8cm,BC=4cm,
∴△BDC的周长是:CD+BD+BC=AD+BD+BC=AB+BC=8+4=12(cm).
故选D.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,已知⊙O是△ABC的外接圆,AB=AC,D是直线BC上一点,直线AD交⊙O于点E,AE=9,DE=3,则AB的长等于( )
如图,已知⊙O是△ABC的外接圆,AB=AC,D是直线BC上一点,直线AD交⊙O于点E,AE=9,DE=3,则AB的长等于( )| A、7 | ||
B、3
| ||
C、2
| ||
D、3
|
把分式
分子、分母中a、b都变成原来的2倍,则分式的值变为原分式值的( )
| 2a |
| a+b |
| A、4倍 | B、2倍 |
| C、不变 | D、0.5 倍 |
下列四个汽车标志图中,中心对称图形是( )
A、 |
B、 |
C、 |
D、 |
不能判定四边形ABCD为平行四边形的条件是( )
| A、AB∥CD,AD=BC |
| B、AB∥CD,∠A=∠C |
| C、AD∥BC,AD=BC |
| D、∠A=∠C,∠B=∠D |
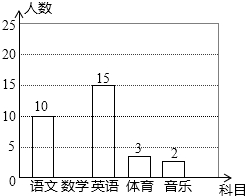 学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下:
学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下: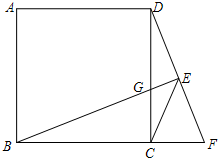 如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.