题目内容
6.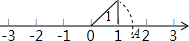 如图所示的数轴上的点A表示的实数是( )
如图所示的数轴上的点A表示的实数是( )| A. | 1.4 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 根据勾股定理求出OA的长,进而可得出结论.
解答 解:∵由图可知,OA=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴点A表示$\sqrt{2}$.
故选C.
点评 本题考查的是实数与数轴,熟知实数与数轴上各点是一一对应关系是解答此题的关键.

练习册系列答案
相关题目
17.下列运算正解的是( )
| A. | $\sqrt{5}$+$\sqrt{7}$=$\sqrt{12}$ | B. | 5+$\sqrt{2}$=5$\sqrt{2}$ | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{{(-2)}^{2}}$=-2 |
1. △ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )
△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )
 △ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )
△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )| A. | 20° | B. | 30° | C. | 45° | D. | 60° |
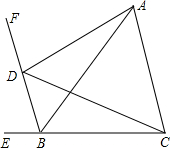 已知,BF平分△ABC的外角ABE,D为BF上一动点.
已知,BF平分△ABC的外角ABE,D为BF上一动点.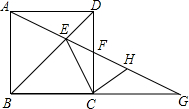 已知正方形ABCD,直线AG分别交BD、CD于点E、F,交BC的延长线于点G,点H是线段FG上的点,且HC⊥CE,求证:点H是GF的中点.
已知正方形ABCD,直线AG分别交BD、CD于点E、F,交BC的延长线于点G,点H是线段FG上的点,且HC⊥CE,求证:点H是GF的中点. 在等腰直角△ABC中,∠ACB=90°,D是AC中点,∠ADF=∠CDB,连接CF交BD于E,求证:BD⊥CF.
在等腰直角△ABC中,∠ACB=90°,D是AC中点,∠ADF=∠CDB,连接CF交BD于E,求证:BD⊥CF.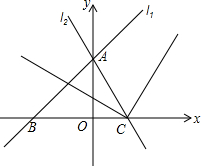 如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.
如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.