题目内容
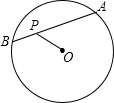 如图,AB是⊙O的一条弦,P是AB上的一点,PA=3,OP=PB=2,则⊙O的半径等于
如图,AB是⊙O的一条弦,P是AB上的一点,PA=3,OP=PB=2,则⊙O的半径等于分析:先求出AB的长,过O作OD⊥AB于点D,连接OB,由垂径定可求出BD的长,进而得出PD的长,再在直角△ODP中利用勾股定理即可求出OD的长.
解答: 解:∵PA=3,OP=PB=2,
解:∵PA=3,OP=PB=2,
∴AB=3+2=5,
过O作OD⊥AB于点D,连接OB,
则BD=
AB=
×5=
,
∵PB=2,
∴PD=
-2=
,
在Rt△ODP中,OD=
=
=
,
在Rt△OBD中,OB=
=
=
.
故答案为:
.
 解:∵PA=3,OP=PB=2,
解:∵PA=3,OP=PB=2,∴AB=3+2=5,
过O作OD⊥AB于点D,连接OB,
则BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵PB=2,
∴PD=
| 5 |
| 2 |
| 1 |
| 2 |
在Rt△ODP中,OD=
| OP2-DP2 |
22-(
|
| ||
| 2 |
在Rt△OBD中,OB=
| OD2+BD2 |
(
|
| 10 |
故答案为:
| 10 |
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
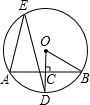 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=25°,则∠OBA的度数是
如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=25°,则∠OBA的度数是 (2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为
(2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 (2008•沈阳)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(2008•沈阳)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上. 如图,AB是⊙O 的一条直径,CD是⊙O的一条弦,交AB与点P,
如图,AB是⊙O 的一条直径,CD是⊙O的一条弦,交AB与点P,