题目内容
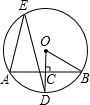如图，AB是⊙O的一条弦，OD⊥AB于点C，交⊙O于点D，点E在⊙O上，∠AED=25°，则∠OBA的度数是分析：连接OA，由圆周角定理可得∠AOB=2∠AED，再由三角形内角和定理及等腰三角形的性质即可求出∠OBA的度数．
解答：
解：连接OA，
∵∠AED=25°，
∴∠AOD=50°，
∵OA=OB，OC⊥AB，
∴∠AOB=2∠AOD=2×50°=100°，
∴∠OAB=∠OBA=
=
=40°．
解：连接OA，∵∠AED=25°，
∴∠AOD=50°，
∵OA=OB，OC⊥AB，
∴∠AOB=2∠AOD=2×50°=100°，
∴∠OAB=∠OBA=
| 180°-∠AOB |
| 2 |
| 180°-100° |
| 2 |
点评：本题考查的是圆周角定理及等腰三角形的性质，解答此题的关键是连接OA，构造出等腰三角形及圆心角，沟通已知角与所求角的关系．
练习册系列答案
相关题目
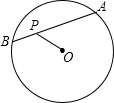如图，AB是⊙O的一条弦，P是AB上的一点，PA=3，OP=PB=2，则⊙O的半径等于
（2013•陕西）如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为
（2008•沈阳）如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．
如图，AB是⊙O 的一条直径，CD是⊙O的一条弦，交AB与点P，