题目内容
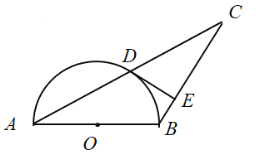
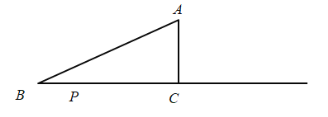
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为射线
为射线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合).
重合).
(1)![]() 为何值时,
为何值时,![]() 最短,求出此时
最短,求出此时![]() 的最小值;
的最小值;
(2)![]() 为何值时,
为何值时,![]() ,说明理由;
,说明理由;
(3)当![]() 的一个顶点与其内心、外心在同一条直线时,直接写出
的一个顶点与其内心、外心在同一条直线时,直接写出![]() 的长.
的长.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 时,
时,![]() ,理由见解析;(3)
,理由见解析;(3)![]() ,8,
,8,![]()
【解析】
(1)当点![]() 在点
在点![]() 时,
时,![]() ,此时
,此时![]() 最短,根据勾股定理求解即可;
最短,根据勾股定理求解即可;
(2)当![]() 时,
时,![]() ,所以
,所以![]() ,再根据已知条件即可判断;
,再根据已知条件即可判断;
(3)根据AB边固定可以分三种情况进行讨论;
解:(1)当点![]() 在点
在点![]() 时,
时,![]() ,此时
,此时![]() 最短.
最短.
在![]() 中,
中,![]()
∴![]() ,
,
![]()
此时![]()
(2)当![]() 时,
时,![]() ,
,
理由:当![]() 时,
时,![]() ,所以
,所以![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]()
(3)当点A与内心、外心重合,△APB是等腰三角形,C为底边的中点,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴BP=2BC=![]() ;
;
当P点与内心、外心重合,△APB是以AB、BP为腰的等腰三角形,
∵AB=8,
∴BP=8;
当点B与内心、外心重合,如图所示,△APB是以![]() 为钝角的三角形,且AP=PB,作
为钝角的三角形,且AP=PB,作![]() ,
,
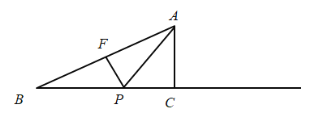
则![]() ,
,
∴![]() ,
,
∵BF=4,AB=8,![]() ,
,
∴![]() ,
,
∴BP= ![]() ;
;
故BP的值为![]() ,8,
,8,![]() .
.

练习册系列答案
相关题目