题目内容
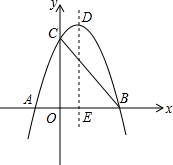 如图,已知二次函数图象y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,且A(-1,0),C(0,3)
如图,已知二次函数图象y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,且A(-1,0),C(0,3)(1)求这个二次函数解析式以及B的坐标;
(2)在(1)中抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若有求出Q的坐标.
考点:二次函数综合题
专题:
分析:(1)把A(-1,0)、C(0,3)两点代入抛物线解析式可得b,c的值,令y=0,可得B点的坐标;
(2)在(1)中抛物线上存在点Q,使△BCQ成为以BC为直角边的直角三角形,有两种可能:B为直角顶点、C为直角顶点,要充分认识△OBC的特殊性,是等腰直角三角形,可以通过解直角三角形求出相关线段的长度.
(2)在(1)中抛物线上存在点Q,使△BCQ成为以BC为直角边的直角三角形,有两种可能:B为直角顶点、C为直角顶点,要充分认识△OBC的特殊性,是等腰直角三角形,可以通过解直角三角形求出相关线段的长度.
解答:解:(1)把A(-1,0)、C(0,3)两点代入抛物线解析式y=-x2+bx+c中得:
,
解得:
,
所以抛物线解析式为:y=-x2+2x+3,
令y=0,
即0=-x2+2x+3,
所以x=-1或3,
即B点的坐标为(3,0);
(2)在(1)中抛物线上存在点Q,使△BCQ成为以BC为直角边的直角三角形,
理由如下:有两种情况:
如图1,过点B作BQ1⊥BC,交抛物线于点Q1、交y轴于点F,连接Q1C.
∵CO=BO=3,
∴∠CBO=45°,
∴∠FBO=45°,BO=OF=3.
∴点F的坐标为(0,-3).
将(0,-3),(3,0)代入y=kx+b得:
,
解
,
∴直线BE的解析式为y=x-3,
由
,
解得
或
,
∴点Q1的坐标为(-2,-5).
如图2,过点C作CF⊥CB,交抛物线于点Q2、交x轴于点F,连接BQ2.
∵∠CBO=45°,
∴∠CFB=45°,OF=OC=3.
∴点F的坐标为(-3,0).
∴直线CF的解析式为y=x+3.
由
解得:
或
,
∴点Q2的坐标为(1,4).
综上,在抛物线上存在点Q1(-2,-5)、Q2(1,4),使△BCQ1、△BCQ2是以BC为直角边的直角三角形.
|
解得:
|
所以抛物线解析式为:y=-x2+2x+3,
令y=0,
即0=-x2+2x+3,
所以x=-1或3,
即B点的坐标为(3,0);
(2)在(1)中抛物线上存在点Q,使△BCQ成为以BC为直角边的直角三角形,
理由如下:有两种情况:
如图1,过点B作BQ1⊥BC,交抛物线于点Q1、交y轴于点F,连接Q1C.

∵CO=BO=3,
∴∠CBO=45°,
∴∠FBO=45°,BO=OF=3.
∴点F的坐标为(0,-3).
将(0,-3),(3,0)代入y=kx+b得:
|
解
|
∴直线BE的解析式为y=x-3,
由
|
解得
|
|
∴点Q1的坐标为(-2,-5).
如图2,过点C作CF⊥CB,交抛物线于点Q2、交x轴于点F,连接BQ2.

∵∠CBO=45°,
∴∠CFB=45°,OF=OC=3.
∴点F的坐标为(-3,0).
∴直线CF的解析式为y=x+3.
由
|
解得:
|
|
∴点Q2的坐标为(1,4).
综上,在抛物线上存在点Q1(-2,-5)、Q2(1,4),使△BCQ1、△BCQ2是以BC为直角边的直角三角形.
点评:此题主要考查了抛物线与x轴的交点以及待定系数法求直线的解析式和等腰直角三角形的性质,解题的关键是利用直线解析式组成方程组求出Q的坐标,题目的难点在于(3)小题中,用到了分类讨论的数学思想,考虑问题要全面,做到不重不漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
x2+1与y=
x2+2的图象的不同之处是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、对称轴 | B、开口方向 |
| C、顶点 | D、形状 |
若方程
=
有增根,则a的值为( )
| x-1 |
| x-2 |
| a |
| 2-x |
| A、2 | B、1 | C、-2 | D、-1 |
若点P(a,-b)在第三象限,则点M(a,-ab)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图所示,已知Rt△ABC中,∠C=90°,AC=
如图所示,已知Rt△ABC中,∠C=90°,AC=| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a为无限不循环小数且a>0,b是a的小数部分,则a-b是( )
| A、无理数 | B、整数 |
| C、有理数 | D、不能确定 |