题目内容
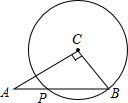 如图所示,已知Rt△ABC中,∠C=90°,AC=
如图所示,已知Rt△ABC中,∠C=90°,AC=| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:垂径定理,勾股定理
专题:
分析:过点C作CD⊥AB于点D,利用勾股定理求出AB的长;运用三角形的面积公式求出△ABC斜边上的高CD;根据垂径定理及勾股定理求出BD的长,即可解决问题.
解答: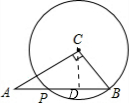 解:如图,过点C作CD⊥PB于点D,则BD=PD;
解:如图,过点C作CD⊥PB于点D,则BD=PD;
∵在Rt△ABC中,∠C=90°,AC=
BC=1,
∴AB=
=
,由面积公式得:
AC•BC=
AB•CD,
∴CD=
=
=
;由勾股定理得:BD=
=
=
=
,
∴AP=AB-2BD=
-
=
.
故选D.
 解:如图,过点C作CD⊥PB于点D,则BD=PD;
解:如图,过点C作CD⊥PB于点D,则BD=PD;∵在Rt△ABC中,∠C=90°,AC=
| 2 |
∴AB=
(
|
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
| ||
|
| ||
| 3 |
12-(
|
1-
|
|
| ||
| 3 |
∴AP=AB-2BD=
| 3 |
2
| ||
| 3 |
| ||
| 3 |
故选D.
点评:该题主要考查了垂径定理、勾股定理的应用问题;解题的关键是过圆心作圆的弦的垂线,构造直角三角形来解题.

练习册系列答案
相关题目
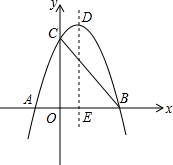 如图,已知二次函数图象y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,且A(-1,0),C(0,3)
如图,已知二次函数图象y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,且A(-1,0),C(0,3)