题目内容
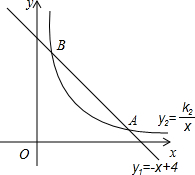 (2013•衢州)如图,函数y1=-x+4的图象与函数y2=
(2013•衢州)如图,函数y1=-x+4的图象与函数y2=| k2 | x |
(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
分析:(1)由函数y1=-x+4的图象与函数y2=
(x>0)的图象交于A(a,1)、B(1,b)两点,把A代入函数y1=-x+4,可求得A的坐标,继而求得函数y2的表达式;
(2)观察图象可得即可求得:当x>0时,y1与y2的大小.
| k2 |
| x |
(2)观察图象可得即可求得:当x>0时,y1与y2的大小.
解答:解:(1)把点A坐标代入y1=-x+4,
得-a+4=1,
解得:a=3,…(1分)
∴A(3,1),
把点A坐标代入y2=
,
∴k2=3,
∴函数y2的表达式为:y2=
; …(3分)
(2)∴由图象可知,
当0<x<1或x>3时,y1<y2,…(4分)
当x=1或x=3时,y1=y2,…(5分)
当1<x<3时,y1>y2. …(6分)
得-a+4=1,
解得:a=3,…(1分)
∴A(3,1),
把点A坐标代入y2=
| k2 |
| x |
∴k2=3,
∴函数y2的表达式为:y2=
| 3 |
| x |
(2)∴由图象可知,
当0<x<1或x>3时,y1<y2,…(4分)
当x=1或x=3时,y1=y2,…(5分)
当1<x<3时,y1>y2. …(6分)
点评:此题考查了一次函数与反比例函数的交点问题.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
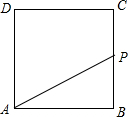 (2013•衢州)如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
(2013•衢州)如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( ) (2013•衢州)如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(
(2013•衢州)如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(
 (2013•衢州)如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边
(2013•衢州)如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边 (2013•衢州)如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
(2013•衢州)如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.