题目内容
 (2013•衢州)如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边
(2013•衢州)如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是
20
20
;四边形A2013B2013C2013D2013的周长是5+5
| ||
| 21005 |
5+5
| ||
| 21005 |
分析:根据菱形的性质以及三角形中位线的性质以及勾股定理求出四边形各边长得出规律求出即可.
解答:解:∵菱形ABCD中,边长为10,∠A=60°,顺次连结菱形ABCD各边中点,
∴△AA1D1是等边三角形,四边形A2B2C2D2是菱形,
∴A1D1=5,C1D1=
AC=5
,A2B2=C2D2=C2B2=A2D2=5,
∴四边形A2B2C2D2的周长是:5×4=20,
同理可得出:A3D3=5×
,C3D3=
C1D1=
×5
,
A5D5=5×(
)2,C5D5=
C1D1=(
)2×5
,
…
∴四边形A2013B2013C2013D2013的周长是:
=
.
故答案为:20,
.
∴△AA1D1是等边三角形,四边形A2B2C2D2是菱形,
∴A1D1=5,C1D1=
| 1 |
| 2 |
| 3 |
∴四边形A2B2C2D2的周长是:5×4=20,
同理可得出:A3D3=5×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
A5D5=5×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
…
∴四边形A2013B2013C2013D2013的周长是:
2(5+5
| ||
| 21006 |
5+5
| ||
| 21005 |
故答案为:20,
5+5
| ||
| 21005 |
点评:此题主要考查了菱形的性质以及矩形的性质和中点四边形的性质等知识,根据已知得出边长变化规律是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
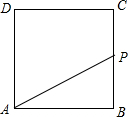 (2013•衢州)如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
(2013•衢州)如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( ) (2013•衢州)如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(
(2013•衢州)如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(
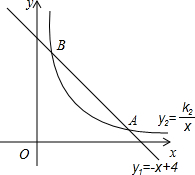 (2013•衢州)如图,函数y1=-x+4的图象与函数y2=
(2013•衢州)如图,函数y1=-x+4的图象与函数y2= (2013•衢州)如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
(2013•衢州)如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.