Question

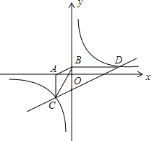
【题目】如图，已知双曲线经过点，点是双曲线第三象限分支上的动点，过点作轴，过点作轴，垂足分别为，，连接，．

求的值；

若的面积为，

①若直线的解析式为，求、的值；

②根据图象，直接写出时的取值范围；

③判断直线与的位置关系，并说明理由．

Answer 1

【答案】；①；②由图象知当或时，；③，理由见解析.

【解析】

（1）把点D的坐标代入双曲线解析式，进行计算即可得解；
（2）①先根据点D的坐标求出BD的长度，再根据三角形的面积公式求出点C到BD的距离，然后求出点C的纵坐标，再代入反比例函数解析式求出点C的坐标，然后利用待定系数法求一次函数解析式解答；
②根据图象即可得到y1>y2时x的取值范围；
③根据题意求出点A、B的坐标，然后利用待定系数由法求出直线AB的解析式，可知与直线CD的解析式k值相等，所以AB、CD平行．

∵双曲线经过点，

∴，

解得；

①设点到的距离为，

∵点的坐标为，轴，

∴，

∴，

解得，

∵点是双曲线第三象限上的动点，点的纵坐标为，

∴点的纵坐标为，

∴，

解得，

∴点的坐标为，

则，

解得；

②由图象知当或时，，

③．

理由如下：∵轴，轴，设点的坐标为，点的坐标为，

∴点、的坐标分别为，，

设直线的解析式为，

则，

解得，

所以，直线的解析式为，

设直线的解析式为，

则，

解得，

∴直线的解析式为，

∵、的解析式都等于，

∴与的位置关系是．