��Ŀ����
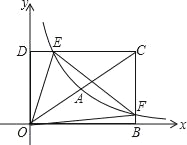
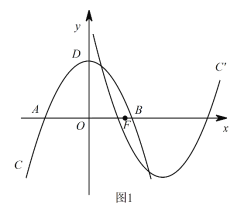
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У�������C��y=ax2+bx+c��x���ཻ��A��B���㣬����ΪD(0��4)��AB=4![]() �����F(m��0)��x�����������һ�㣬��������C�Ƶ�F��ת180�����õ��µ�������C/��
�����F(m��0)��x�����������һ�㣬��������C�Ƶ�F��ת180�����õ��µ�������C/��
(1)��������C�ĺ�������ʽ��
(2)��������C/��������C��y����Ҳ���������ͬ�Ĺ����㣬��m��ȡֵ��Χ��
(3)��ͼ2��P�ǵ�һ������������C��һ�㣬������������ľ�����ȣ���P��������C/�ϵĶ�Ӧ��P/����M��C�ϵĶ��㣬N��C/�ϵĶ��㣬��̽���ı���PMP/N�ܷ��Ϊ�����Σ����ܣ���ֱ��д��m��ֵ�������ܣ���˵�����ɣ�

���𰸡���1��![]() ����2��2��m��
����2��2��m��![]() ����3��m=6��m=
����3��m=6��m=![]() ��3��
��3��
��������
���⣨1�������������ߵĶ���C��0��4����A��![]() ��0�����������ߵĽ���ʽΪ
��0�����������ߵĽ���ʽΪ![]() ����A��
����A��![]() ��0������ɵ�a=
��0������ɵ�a=![]() ���ɴ˼��ɽ�����⣻
���ɴ˼��ɽ�����⣻
��2��������������C���Ķ�������Ϊ��2m����4������������C���Ľ���ʽΪ![]() ����
���� ����ȥy�õ�
����ȥy�õ�![]() �������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����
�������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����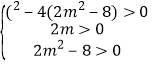 ���ⲻ��ʽ�鼴�ɽ�����⣻
���ⲻ��ʽ�鼴�ɽ�����⣻
��3������1���ı���PMP��N�ܳ�Ϊ�����Σ���PE��x����E��MH��x����H����������֪P��2��2��������PFM�ǵ���ֱ��������ʱ���ı���PMP��N�������Σ��Ƴ�PF=FM����PFM=90�㣬��֤��PFE�ա�FMH���ɵ�PE=FH=2��EF=HM=2��m���ɵ�M��m+2��m��2�������ɴ���ϵ�������ɽ�����⣻����2����ͼ���ı���PMP��N�������Σ�ͬ���ɵ�M��m��2��2��m�������ô���ϵ�������ɽ�����⣮
�����������1�������������ߵĶ���C��0��4����A��![]() ��0�����������ߵĽ���ʽΪ
��0�����������ߵĽ���ʽΪ![]() ����A��
����A��![]() ��0������ɵ�a=
��0������ɵ�a=![]() ����������C�ĺ�������ʽΪ
����������C�ĺ�������ʽΪ![]() ��
��
��2��������������C���Ķ�������Ϊ��2m����4������������C���Ľ���ʽΪ![]() ����
����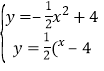 ����ȥy�õ�
����ȥy�õ�![]() �������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����
�������⣬������C����������C��y����Ҳ���������ͬ�Ĺ����㣬����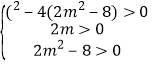 �����2��m��
�����2��m��![]() ��������������m��ȡֵ��ΧΪ2��m��
��������������m��ȡֵ��ΧΪ2��m��![]() ��
��
��3�����ۣ��ı���PMP��N�ܳ�Ϊ�����Σ�
���ɣ�1����1����ͼ����PE��x����E��MH��x����H��
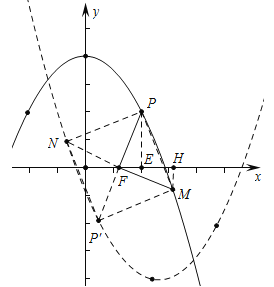
��������֪P��2��2��������PFM�ǵ���ֱ��������ʱ���ı���PMP��N�������Σ���PF=FM����PFM=90�㣬��֤��PFE�ա�FMH���ɵ�PE=FH=2��EF=HM=2��m����M��m+2��m��2�����ߵ�M��![]() �ϣ���
�ϣ���![]() �����m=
�����m=![]() ��3��
��3��![]() ��3������������m=
��3������������m=![]() ��3ʱ���ı���PMP��N�������Σ�
��3ʱ���ı���PMP��N�������Σ�
����2����ͼ���ı���PMP��N�������Σ�ͬ���ɵ�M��m��2��2��m������M��m��2��2��m������![]() �У�
�У�![]() �����m=6��0������������m=6ʱ���ı���PMP��N�������Σ�
�����m=6��0������������m=6ʱ���ı���PMP��N�������Σ�
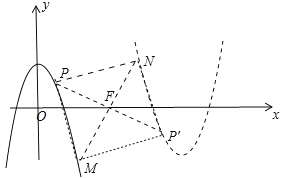
����������m=6��m=![]() ��3ʱ���ı���PMP��N�������Σ�
��3ʱ���ı���PMP��N�������Σ�

 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�