题目内容
5.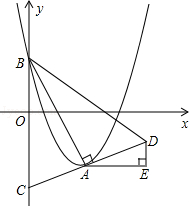 如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m(m>0)的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m(m>0)的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.(1)若m=2,则点A的坐标为(2,-2),点B的坐标为(0,2);
(2)随着m的变化,DE的长是否发生变化?如果不变,请求出DE的长;如果变化,请说明理由;
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?
②过点D作AB的平行线,与第(3)题第①题确定的函数图象的另一个交点为P,当m为何值时,四边形ABDP是平行四边形?
分析 (1)把m=2代入到抛物线的解析式中,计算A和B的坐标即可;
(2)先证明△AFC≌△AED(AAS),得AF=AE,并根据解析式求出AF=AE=|m|=m,OB=m,再证明△FAB∽△EDA,列比例式为$\frac{BF}{AE}=\frac{AF}{DE}$,求DE=1;
(3)①表示点D的坐标为(2m,-m2+m+1),列方程组可求y关于x的函数关系式;
②作PQ⊥DE于点Q,则△DPQ≌△BAF,然后分两种情况:表示点P的坐标,代入y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+1解答.
解答 解:(1)当m=2时,y=(x-m)2-m2+m=(x-2)2-4+2=(x-2)2-2=x2-4x+2,
∴点A的坐标为(2,-2),点B的坐标为(0,2),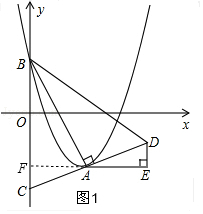
故答案为:(2,-2),(0,2);
(2)随着m的变化,DE的长不发生变化,理由是:
y=(x-m)2-m2+m=x2-2mx+m,
A(m,-m2+m),B(0,m),
如图1,延长AE交BC于F,
∴∠AFC=∠AED=90°,
在△AFC和△AED中,
∵$\left\{\begin{array}{l}{∠AFC=∠AED}\\{∠CAF=∠DAE}\\{AC=AD}\end{array}\right.$,
∴△AFC≌△AED(AAS),
∴AF=AE,∠ACB=∠ADE,
当x=m时,y=-m2+m,
当x=0时,y=m,
∴AF=AE=|m|=m,
∵∠ABF=90°-∠ACB=90°-∠ADE=∠DAE,
∵∠AFB=∠AED=90°,
∴△FAB∽△EDA,
∴$\frac{BF}{AE}=\frac{AF}{DE}$,
∵BF=OF+OB=m+m2-m=m2,
∴$\frac{{m}^{2}}{m}=\frac{m}{DE}$,
∴DE=1,
∴随着m的变化,DE的长不发生变化;
(3)①由(2)得:A(m,-m2+m),
AF=AE=|m|=m,DE=1,
∴D(2m,-m2+m+1),
∵设点D的坐标为(x,y),
∴$\left\{\begin{array}{l}{x=2m}\\{y=-{m}^{2}+m+1}\end{array}\right.$,
m=$\frac{1}{2}$x,
∴y=-$(\frac{1}{2}x)^{2}$+$\frac{1}{2}$x+1=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+1;
②作PQ⊥DE于点Q,则△DPQ≌△BAF,
(Ⅰ)当四边形ABDP为平行四边形时(如图2),
点P的横坐标为3m,
点P的纵坐标为:(-m2+m+1)-m2=-2m2+m+1,
把P(3m,-2m2+m+1)的坐标代入y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+1得:
-2m2+m+1=-$\frac{1}{4}$×(3m)2+$\frac{1}{2}$×(3m)+1,
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=2.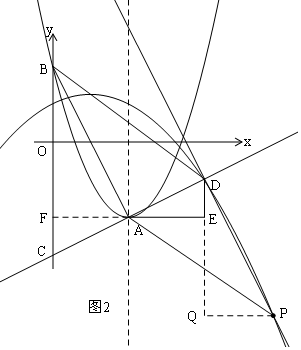
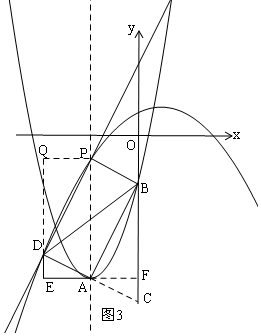
(Ⅱ)当四边形ABPD为平行四边形时(如图3),
点P的横坐标为m,
点P的纵坐标为:(-m2+m+1)+m2=m+1,
把P(m,m+1)的坐标代入y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+1得:
m+1=-$\frac{1}{4}$m2+$\frac{1}{2}$m+1,
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=-2,
综上所述:m的值为2或-2.
点评 本题是二次函数综合题,考查了利用一点求二次函数的解析式、平行四边形的性质、三角形全等的性质和判定及点与坐标特点等知识,难度适中,解答时要注意数形结合及分类讨论.

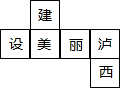 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 泸 | D. | 西 |
| A. | 正方形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
| A. | 第一、二、三象限 | B. | 第一、三、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
| A. | a是无理数 | B. | a是方程x2-3=0的解 | ||
| C. | a是8的算术平方根 | D. | 2<a<4 |
| A. | 2x-x=2 | B. | (ab2)3=ab8 | C. | a•a4=a5 | D. | (-a+b)2=(a+b)2 |
| A. | 3cm、4cm、8cm | B. | 5cm、5cm、10cm | C. | 12cm、5cm、6cm | D. | 8cm、6cm、4cm |