题目内容
如图，边长为1的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________．
分析：连接BP，作EF⊥BC于点F，由正方形的性质可知△BEF为等腰直角三角形，BE=1，可求EF，利用面积法得S△BPE+S△BPC=S△BEC，将面积公式代入即可．
解答：
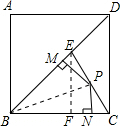解：连接BP，作EF⊥BC于点F，则∠EFB=90°，由正方形的性质可知∠EBF=45°，
∴△BEF为等腰直角三角形，
又根据正方形的边长为1，得到BE=BC=1，
在直角三角形BEF中，sin∠EBF=
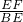，即BF=EF=BEsin45°=1×
=，又PM⊥BD，PN⊥BC，
∴S△BPE+S△BPC=S△BEC，
即
BE×PM+×BC×PN=BC×EF，∵BE=BC，
PM+PN=EF=
；故答案为：
．点评：解决本题的关键是作出辅助线，构造矩形和全等三角形，把所求的线段转移到正方形的对角线上．
练习册系列答案
相关题目
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
轴正方向连续翻转2006次，点P依次落在点
，
，
，
，……
的位置，则
＝_________．
