��Ŀ����
�ڡ�O�У�ABΪ��Oֱ����PC������O��CΪAB���ӳ�����һ�㣬PD��DC=2��3����P��AB���߽��ڵ�F������OD��PF�ڵ�E������CE��QΪ��O��һ�㣬����OQ��EQ��QP��OC=5��DC=3��ECΪ��PCA�Ľ�ƽ������FC=CD��
��1�����O�뾶��
��2������QOD=90��ʱ��AB����һ��G����PG+QG����Сֵ��
��3��S��PQE�Ƿ�������ֵ�������ڣ���д��S��PQE�����ֵ���������ڣ���˵�����ɣ�

��1�����O�뾶��
��2������QOD=90��ʱ��AB����һ��G����PG+QG����Сֵ��
��3��S��PQE�Ƿ�������ֵ�������ڣ���д��S��PQE�����ֵ���������ڣ���˵�����ɣ�

���㣺Բ���ۺ���
ר�⣺
��������1�����ж���CDOΪֱ�������Σ��������DO�ij������ɽ��⣻
��2���ҵ���Q����AB�ĶԳƵ�Q'������PQ'��AB��G������OQ'����Q'M��PF����OH��Q'M�����ı���ONQ'H���ı���OFMH��Ϊ���Σ���֤sin��DCO=sin��QOA����OQ'H=��AOQ'����AOQ'=��AOQ���������OH��Q'H�ij����������Q'M��PM�ij������ݹ��ɶ����������PQ'�ij������ɽ��⣻
��3������2���ǵ����к���ֵ���㹫ʽ�������tan��ECF=
���������PE��ֵ������S��PQE�������ֵΪ��Q�͵�A�غ�ʱ���������S��PQE��ֵ�����ɽ��⣮
��2���ҵ���Q����AB�ĶԳƵ�Q'������PQ'��AB��G������OQ'����Q'M��PF����OH��Q'M�����ı���ONQ'H���ı���OFMH��Ϊ���Σ���֤sin��DCO=sin��QOA����OQ'H=��AOQ'����AOQ'=��AOQ���������OH��Q'H�ij����������Q'M��PM�ij������ݹ��ɶ����������PQ'�ij������ɽ��⣻
��3������2���ǵ����к���ֵ���㹫ʽ�������tan��ECF=
| 1 |
| 2 |
����⣺��1����PC���O���У�
��OD��PC��
��CO=5��CD=3��
��DO2=CO2-CD2=16��
��OD=4��
���O�뾶Ϊ4��
��2���ҵ���Q����AB�ĶԳƵ�Q'������PQ'��AB��G������OQ'����Q'M��PF����OH��Q'M�����ı���ONQ'H���ı���OFMH��Ϊ���Σ�
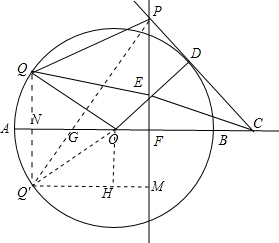
�ߡ�QOD=90�㣬��PDO=90�㣬
��OQ��PC��
���QOA=��DCO��
��sin��DCO=sin��QOA=
=
��
�ߡ�OQ'H=��AOQ'����AOQ'=��AOQ��
��OH=OQ'•sin��OQ'H=
��
��Q'H=
��
��CO=5��CF=CD=3��
��OF=2��
��HM=2��
��Q'M=Q'H+HM=
��
��PF��CF��PC=5��CF=3��
��PF=4��
��PM=PF+MF=PF+OH=
��
��RT��PMQ'��PQ'2=PM2+Q'M2��
��PQ'=
��
��PG+QG����Сֵ=PQ'=
��
��3����ECΪ��PCA�Ľ�ƽ���ߣ�
��tan��OCD=
��
��tan��ECF=
��
��EF=CF•tan��ECF=
��
��PE=PF-EF=
��
��S��PQE�������ֵΪ��Q�͵�A�غ�ʱ��
S��PQE=
PE•AF=
��
����4+2��=
��
��OD��PC��
��CO=5��CD=3��
��DO2=CO2-CD2=16��
��OD=4��
���O�뾶Ϊ4��
��2���ҵ���Q����AB�ĶԳƵ�Q'������PQ'��AB��G������OQ'����Q'M��PF����OH��Q'M�����ı���ONQ'H���ı���OFMH��Ϊ���Σ�

�ߡ�QOD=90�㣬��PDO=90�㣬
��OQ��PC��
���QOA=��DCO��
��sin��DCO=sin��QOA=
| DO |
| CO |
| 4 |
| 5 |
�ߡ�OQ'H=��AOQ'����AOQ'=��AOQ��
��OH=OQ'•sin��OQ'H=
| 16 |
| 5 |
��Q'H=
| 12 |
| 5 |
��CO=5��CF=CD=3��
��OF=2��
��HM=2��
��Q'M=Q'H+HM=
| 22 |
| 5 |
��PF��CF��PC=5��CF=3��
��PF=4��
��PM=PF+MF=PF+OH=
| 36 |
| 5 |
��RT��PMQ'��PQ'2=PM2+Q'M2��
��PQ'=
2
| ||
| 5 |
��PG+QG����Сֵ=PQ'=
2
| ||
| 5 |
��3����ECΪ��PCA�Ľ�ƽ���ߣ�
��tan��OCD=
| 2tan��ECF |
| 1-(tan��ECF)2 |
��tan��ECF=
| 1 |
| 2 |
��EF=CF•tan��ECF=
| 3 |
| 2 |
��PE=PF-EF=
| 5 |
| 2 |
��S��PQE�������ֵΪ��Q�͵�A�غ�ʱ��
S��PQE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
���������⿼����ֱ�������������Ǻ�����Ӧ�ã������˹��ɶ��������ã�������2���ǵ����к���ֵ������������������ļ��㣬���������PE�ij��ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
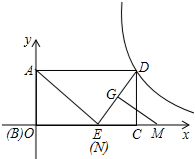 ��ͼ����ƽ��ֱ������ϵ�У���֪����ABCD��E��BC��һ�㣬��AED=90�㣬AB=6��SIN��AEB=
��ͼ����ƽ��ֱ������ϵ�У���֪����ABCD��E��BC��һ�㣬��AED=90�㣬AB=6��SIN��AEB= ��ͼ����ABC�У�AD�����ߣ�AE�ǽ�ƽ���ߣ�CF��AE��F��AB=10��AC=6����DF�ij�Ϊ
��ͼ����ABC�У�AD�����ߣ�AE�ǽ�ƽ���ߣ�CF��AE��F��AB=10��AC=6����DF�ij�Ϊ ��ͼ��CD��AB��AB�AAE�����ABC+��BCD��
��ͼ��CD��AB��AB�AAE�����ABC+��BCD�� ��֪���κ���y=x2+bx-1��ͼ���㣨3��2����
��֪���κ���y=x2+bx-1��ͼ���㣨3��2����