题目内容
 如图,等腰Rt△ABC,∠ACB=90°,B、C均在y轴的正半轴上,且B点坐标为(0,3
如图,等腰Rt△ABC,∠ACB=90°,B、C均在y轴的正半轴上,且B点坐标为(0,3| 2 |
| k |
| x |
| A、-3 | ||
| B、-4 | ||
C、-3
| ||
D、-4
|
考点:反比例函数图象上点的坐标特征,等腰直角三角形
专题:
分析:令C(0,h)则点A为(-3
+h,h),点A在反比例函数上,则(-3
+h)•h=k,再根据点D是AD的中点得出D点坐标,代入反比例函数的解析式,两式联立即可得出k的值.
| 2 |
| 2 |
解答:解:令C(0,h)则点A为(-3
+h,h),点A在反比例函数上,则(-3
+h)•h=k①,
∵D为AB中点,
∴D(
,
),
∵D点在反比例函数的图象上,
∴
•
=k②,
①②联立得,h=
,k=-4.
故选B.
| 2 |
| 2 |
∵D为AB中点,
∴D(
-3
| ||
| 2 |
3
| ||
| 2 |
∵D点在反比例函数的图象上,
∴
-3
| ||
| 2 |
3
| ||
| 2 |
①②联立得,h=
| 2 |
故选B.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
下列各点在一次函数y=2x-1的图象上的是( )
| A、(0,-1) |
| B、(2,-1) |
| C、(1,0) |
| D、(2,1) |
下列计算正确的是( )
| A、(a3)3=a6 |
| B、a3•a3=a9 |
| C、a3+a3=2a6 |
| D、a2•(a3)2=a8 |
若代数式a2-( )a+16是一个多项式的完全平方,则括号里的数是( )
| A、4 | B、±4 | C、-6 | D、±8 |
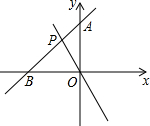 如图,直线y1=kx+b过点A(0,2)且与直线y2=mx交于点P(-1,-m),则关于x的不等式组mx>kx+b>mx-2的解集为( )
如图,直线y1=kx+b过点A(0,2)且与直线y2=mx交于点P(-1,-m),则关于x的不等式组mx>kx+b>mx-2的解集为( )| A、x<-1 |
| B、-2<x<0 |
| C、-2<x<-1 |
| D、x<-2 |
下列四个图中∠1=∠2一定成立的是( )
A、 |
B、 |
C、 |
D、 |
北京故宫的占地面积约为7.20×105米2,下列说法正确的是( )
| A、有两个有效数字,精确到十分位 |
| B、有两个有效数字,精确到万位 |
| C、有三个有效数字,精确到百分位 |
| D、有三个有效数字,精确到千位 |
-6+5的结果是( )
| A、-11 | B、1 | C、-1 | D、11 |
 某学校的围墙CD到教学楼AB的距离CE=22.5米,CD=3米.该学校为了纪念建校61周年准备彩旗连接线AC,∠ACE=22°.
某学校的围墙CD到教学楼AB的距离CE=22.5米,CD=3米.该学校为了纪念建校61周年准备彩旗连接线AC,∠ACE=22°.