题目内容
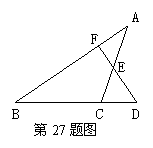
如图,已知D为△ABC边BC延长线上一点,DF⊥A
B于F交AC于E,∠A
=35°,∠D=42°,求∠ACD的度数.
 |
解:因为∠AFE=90°,所以∠AEF=90°-∠A=90°-35°=55°.所以∠CED=∠AEF=55°,
所以∠ACD=180°-∠CED-∠D=180°-55°-42=83°.
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
名校名师培优作业本加核心试卷系列答案全程金卷系列答案
3、如图，已知⊙O，AB为直径，AB⊥CD，垂足为E，由图你还能知道哪些正确的结论请把它们一一写出来
如图，已知AD为△ABC的角平分线，DE∥AB，如果
（2011•成华区二模）如图，已知半径为R的⊙O1的直径AB和弦CD交于点M，点A为
（2012•苏州）如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x（2＜x＜4）．