题目内容
已知x、y、z为三个非负实数,且满足3x+2y+z=5,2x+y-3z=1,若u=3x+y-7z,则u的最大值与最小值之和为
- A.

- B.

- C.

- D.

A
分析:首先把3x+2y+z=5,2x+y-3z=1,组成方程组,分别用含z的代数式表示x和y,再代入u=3x+y-7z中,可得到u=3z-2,再由条件x、y为三个非负实数分别表示出其取值范围,便得到z的取值范围,亦可得到u的取值范围,即可以得到答案.
解答:∵ .
.
∴ ,
,
∵u=3x+y-7z,
∴u=3(7z-3)+(-11z+7)-7z=3z-2,
由x≥0,y≥0得:
解得: ,
,
∴3× -2≤3z-2≤3×
-2≤3z-2≤3× -2,
-2,
即 ,
,
∴u最小=- ,u最大=
,u最大= ,
,
∴u最小+u最大=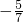 +(
+( )=-
)=- .
.
故选A.
点评:此题主要考查了方程组与不等式的综合运用,做题的关键是用含z的代数式分别表示出x,y,然后根据已知条件表示出u的取值范围,综合性较强.
分析:首先把3x+2y+z=5,2x+y-3z=1,组成方程组,分别用含z的代数式表示x和y,再代入u=3x+y-7z中,可得到u=3z-2,再由条件x、y为三个非负实数分别表示出其取值范围,便得到z的取值范围,亦可得到u的取值范围,即可以得到答案.
解答:∵
 .
.∴
 ,
,∵u=3x+y-7z,
∴u=3(7z-3)+(-11z+7)-7z=3z-2,
由x≥0,y≥0得:

解得:
 ,
,∴3×
 -2≤3z-2≤3×
-2≤3z-2≤3× -2,
-2,即
 ,
,∴u最小=-
 ,u最大=
,u最大= ,
,∴u最小+u最大=
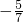 +(
+( )=-
)=- .
.故选A.
点评:此题主要考查了方程组与不等式的综合运用,做题的关键是用含z的代数式分别表示出x,y,然后根据已知条件表示出u的取值范围,综合性较强.

练习册系列答案
相关题目