题目内容
如图，已知△ABC内接于⊙O，直线DE与⊙O相切于点A，BD∥CA，求证：AB•DA=BC•BD．
分析：欲证AB•DA=BC•BD，即证AB：BD=BC：DA，即证△ABC∽△BDA．根据已知条件，△ABC与△BDA中，有两角对应相等，由相似三角形的判定，它们相似．
解答：
证明：∵DE与⊙O相切，
∴∠C=∠1，
∵BD∥CA，∴∠2=∠3．
∴△ABC∽△BDA．
∴
=
．
∴AB•DA=BC•BD．
证明：∵DE与⊙O相切，∴∠C=∠1，
∵BD∥CA，∴∠2=∠3．
∴△ABC∽△BDA．
∴
| AB |
| BD |
| BC |
| DA |
∴AB•DA=BC•BD．
点评：本题考查相似三角形的判定定理：有两角对应相等的两个三角形相似．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
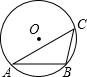如图，已知△ABC内接于⊙O，∠C=45°，AB=4，则⊙O的半径为
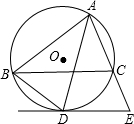如图，已知△ABC内接于⊙O，AD平分∠BAC，交⊙O于点D，过D作⊙O的切线与AC的延长线交于点E．
（2013•樊城区模拟）如图，已知△ABC内接于⊙O，弦AD交BC于E，过点D的切线MN交直线AB于M，交直线AC于N．
如图，已知△ABC内接于⊙O，AE平分∠BAC，且AD⊥BC于点D，连接OA．
如图，已知△ABC内接于⊙O，AB=AC，∠A=36°，CD是⊙O的直径，求∠ACD的度数．