题目内容
 如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=
如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:先由正方形ADEF的面积为4,得出边长为2,BF=2AF=4,AB=AF+BF=2+4=6.再设B点坐标为(t,6),则E点坐标(t-2,2),根据点B、E在反比例函数y=
的图象上,利用根据反比例函数图象上点的坐标特征得k=6t=2(t-2),即可求出k=-6.
| k |
| x |
解答:解:∵正方形ADEF的面积为4,
∴正方形ADEF的边长为2,
∴BF=2AF=4,AB=AF+BF=2+4=6.
设B点坐标为(t,6),则E点坐标(t-2,2),
∵点B、E在反比例函数y=
的图象上,
∴k=6t=2(t-2),
解得t=-1,k=-6.
故答案为-6.
∴正方形ADEF的边长为2,
∴BF=2AF=4,AB=AF+BF=2+4=6.
设B点坐标为(t,6),则E点坐标(t-2,2),
∵点B、E在反比例函数y=
| k |
| x |
∴k=6t=2(t-2),
解得t=-1,k=-6.
故答案为-6.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知x=-1是方程x2+mx+1=0的一个实数根,则m的值是( )
| A、0 | B、1 | C、2 | D、-2 |
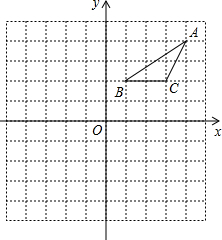 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: 如图,AB∥CD∥EF,∠BEF=120°,∠BCD=100°,则∠CBE=
如图,AB∥CD∥EF,∠BEF=120°,∠BCD=100°,则∠CBE= 如图,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走了2015米停下,则这个微型机器人停在
如图,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走了2015米停下,则这个微型机器人停在