题目内容
计算:
(1)(-99
)×5;
(2)-12-(-10)÷
×2÷(-4)2;
(3)(
-3+
-
)÷(-
);
(4)(-
)2÷(
)3-12×(
-
).
(1)(-99
| 24 |
| 25 |
(2)-12-(-10)÷
| 1 |
| 2 |
(3)(
| 1 |
| 2 |
| 5 |
| 6 |
| 7 |
| 12 |
| 1 |
| 36 |
(4)(-
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 6 |
考点:有理数的混合运算
专题:计算题
分析:(1)原式变形后,利用乘法分配律计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式利用除法法则变形,再利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式利用除法法则变形,再利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答:解:(1)原式=(-100+
)×5=-500+
=-499
;
(2)原式=-1+40÷16=-1+2.5=1.5;
(3)原式=(
-3+
-
)×(-36)=-18+108-30+21=81;
(4)原式=3-9+2=-4.
| 1 |
| 25 |
| 1 |
| 5 |
| 4 |
| 5 |
(2)原式=-1+40÷16=-1+2.5=1.5;
(3)原式=(
| 1 |
| 2 |
| 5 |
| 6 |
| 7 |
| 12 |
(4)原式=3-9+2=-4.
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
要使分式
有意义,则x的取值范围是( )
| 3x |
| 3x+7 |
A、x=
| ||
B、x>
| ||
C、x<
| ||
D、x≠-
|
 如图,在直角梯形ABCD中,∠ABC=90°,AD=2,BC=4,高DF=2,求腰DC的长.
如图,在直角梯形ABCD中,∠ABC=90°,AD=2,BC=4,高DF=2,求腰DC的长. 若每个小正方形边长为1分米,共摆放了8层,现要将靠墙及地面的部分涂上防锈漆,求防锈漆的总面积.
若每个小正方形边长为1分米,共摆放了8层,现要将靠墙及地面的部分涂上防锈漆,求防锈漆的总面积.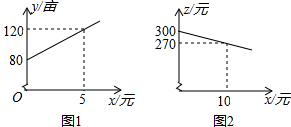 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.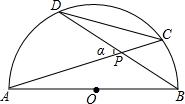 如图,C、D是以AB为直径的半圆上的两个点(不与A、B重合),连接DC、AC、DB,AC与BD交于点P,若∠APD=α,则
如图,C、D是以AB为直径的半圆上的两个点(不与A、B重合),连接DC、AC、DB,AC与BD交于点P,若∠APD=α,则