题目内容
如图，△ABC与△A′B′C′是位似图形，且位似比是1：2．（1）在图中画出位似中心点O．
（2）若AB=2cm，则A′B′的长为多少？
考点：作图-位似变换
专题：作图题
分析：（1）根据位似图形的性质直接得出位似中心即可；
（2）利用位似比得出对应边的比进而得出答案．
（2）利用位似比得出对应边的比进而得出答案．
解答：
解：（1）如图所示：连接BB′、CC′，它们的交点即为位似中心O；
（2）∵△ABC与△A′B′C′是位似图形，且位似比是1：2，
AB=2cm，
∴A′B′的长为4 cm．
解：（1）如图所示：连接BB′、CC′，它们的交点即为位似中心O；（2）∵△ABC与△A′B′C′是位似图形，且位似比是1：2，
AB=2cm，
∴A′B′的长为4 cm．
点评：此题主要考查了位似图形的性质，利用位似比等于对应边的比得出是解题关键．
练习册系列答案
相关题目
下列方程中，一元二次方程是（ ）
A、x2+
| ||
| B、ax2+bx=0 | ||
| C、x2=0 | ||
| D、3x2-2xy-5y2=0 |
方程组
的解是（ ）
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
在如图的正方形网格中画出以下三角形（要有答，并把各边的长写在边上）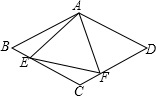
如图，在菱形ABCD中，E，F分别是BC，CD上的点，∠B=∠EAF=60°，∠BAE=20°，求∠CEF的度数．