题目内容
1.将分式$\frac{5x-4}{(x-1)(2x-1)}$表示成部分分式.分析 令$\frac{5x-4}{(x-1)(2x-1)}$=$\frac{A}{x-1}$+$\frac{B}{2x-1}$,把异分母分式的加减法转化为同分母分式的加减法,然后根据等号左右两边分式的分子相同,列出关于A、B的二元一次方程组,再解方程组,求出A、B的值是多少即可.
解答 解:令$\frac{5x-4}{(x-1)(2x-1)}$=$\frac{A}{x-1}$+$\frac{B}{2x-1}$,
∵$\frac{A}{x-1}$+$\frac{B}{2x-1}$=$\frac{A(2x-1)}{(x-1)(2x-1)}$+$\frac{B(x-1)}{(x-1)(2x-1)}$=$\frac{(2A+B)x-(A+B)}{(x-1)(2x-1)}$,
∴$\left\{\begin{array}{l}{2A+B=5}\\{A+B=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{A=1}\\{B=3}\end{array}\right.$,
∴$\frac{5x-4}{(x-1)(2x-1)}$=$\frac{1}{x-1}$+$\frac{3}{2x-1}$.
点评 此题主要考查了异分母分式加减法的运算法则,要熟练掌握,解答此题的关键是熟练掌握通分的方法,把异分母分式的加减法转化为同分母分式的加减法.此题还考查了二元一次方程组的求解方法,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在数轴上,到表示1的点的距离等于6的点表示的数是( )
| A. | -5 | B. | 7 | C. | -5或7 | D. | 5 |
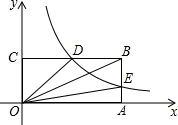 如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3,已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过BC边上的中点D,交AB于点E
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3,已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过BC边上的中点D,交AB于点E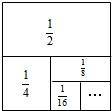 利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?