��Ŀ����
��ͼ���Ѿ���OABC������ֱ������ϵ�У�OA=6��OC=8�����������۵���ʹ��B��O�غϣ��õ��ۺ�EF��
��1������ͨ�� �취��ʹ�ı���AEFO�䵽�ı���BEFC��λ�ã��ƽ�ơ�������ת����ת������
��2��д����E������ϵ�е�λ�ü���E������ ��
��3���ۺ�EF�ij�Ϊ ��
��4����ֱ��l�Ѿ���OABC������ֳ���ȵ������֣���ֱ��l�ؾ����� ��д��������������һ��ֱ�ߵĺ�����ϵʽ ��
��1������ͨ�� �취��ʹ�ı���AEFO�䵽�ı���BEFC��λ�ã��ƽ�ơ�������ת����ת������
��2��д����E������ϵ�е�λ�ü���E������ ��
��3���ۺ�EF�ij�Ϊ ��
��4����ֱ��l�Ѿ���OABC������ֳ���ȵ������֣���ֱ��l�ؾ����� ��д��������������һ��ֱ�ߵĺ�����ϵʽ ��

| �⣺��EF��OB�ཻ�ڵ�N�� �������۵� ��EF��OB��ON=NB�� �֡߾���OABC�� ��AB��OC�� ���OFE=��BEF�� �֡�FNO=��ENB��ON=BN�� ���OFN�ա�EBN�� ��FN=EN��OF=BE�� ���ı���OABC�Ǿ��� ���FOB=��OBA ���OFN�ס�OAB ��  �֡�֪��AB=8��OA=6 ��FN=3.75 ��EF=7.5 ��OF=BE=6.25 ��AE=8��6.25=1.75 �ߵ�E�ڵ�һ������ ���E��6��1.75���� ������ֱ֪��L�ؾ������εĶԽ��߽��� ���������佻�����������Ϊ���ο���һ�뼴Ϊ3��������Ϊ���γ���һ��Ϊ4�� ��������һ��ֱ�߾���ԭ�㼴��Ϊy=kx���루3��4����y=  x�� x�� �ʴ�Ϊ����1����ת����2����6 ��1.75 ������3��7.5����4����3 ��4����  �� �� |
 |

��ϰ��ϵ�д�
�����Ŀ
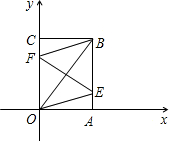 ���ۺ�EF������OE��BF��
���ۺ�EF������OE��BF��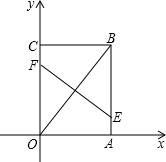 ���ۺ�EF��
���ۺ�EF�� 21����ͼ���Ѿ���OABC����ֱ������ϵ�У�OC��x���ϣ�OA��y���ϣ���OC=2��OA=4���Ѿ���OABC����ԭ��˳ʱ����ת90��õ�����OA��B��C�䣬���B�������Ϊ��������
21����ͼ���Ѿ���OABC����ֱ������ϵ�У�OC��x���ϣ�OA��y���ϣ���OC=2��OA=4���Ѿ���OABC����ԭ��˳ʱ����ת90��õ�����OA��B��C�䣬���B�������Ϊ�������� ��ͼ���Ѿ���OABC����ֱ������ϵ�У�OC��x���ϣ�OA��y���ϣ���OC=2��OA=4���Ѿ���OABC����ԭ��˳ʱ����ת90��õ�����ODEF����E������Ϊ��������
��ͼ���Ѿ���OABC����ֱ������ϵ�У�OC��x���ϣ�OA��y���ϣ���OC=2��OA=4���Ѿ���OABC����ԭ��˳ʱ����ת90��õ�����ODEF����E������Ϊ��������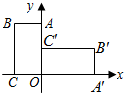 17����ͼ���Ѿ���OABC����ֱ������ϵ�У�OC��x���ϣ�OA��y���ϣ���OC=1��OA=2���Ѿ���OABC����ԭ��˳ʱ����ת90��õ�����OA'B'C'�����B'������Ϊ
17����ͼ���Ѿ���OABC����ֱ������ϵ�У�OC��x���ϣ�OA��y���ϣ���OC=1��OA=2���Ѿ���OABC����ԭ��˳ʱ����ת90��õ�����OA'B'C'�����B'������Ϊ