题目内容
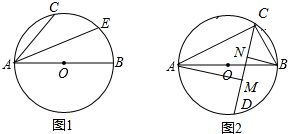
4.已知AB为⊙O的直径,AB=10,AC为弦.(1)如图1,弦AE平分∠CAB,AC=6,求AE的长.
(2)如图2,弦CD平分∠ACB,AM⊥CD于M,BN⊥CD于N,若$\frac{AM}{BN}$=$\frac{4}{3}$,求CD的长.
分析 (1)连接BE,连接BC交AE于G,根据圆周角定理和勾股定理以及角平分线的性质证明△CAG∽△EAB,根据相似三角形的性质得到答案;
(2)连接OD,作OF⊥CD于F,根据平行线的性质求出AP、PB、OP的长,根据角平分线的性质得到$\frac{AC}{BC}$=$\frac{AP}{BP}$=$\frac{4}{3}$,求出AC,得到AM的长,根据勾股定理计算即可.
解答 解:(1)连接BE,连接BC交AE于G,
∵AB为⊙O的直径,
∴∠ACB=∠AEB=90°,
∵AB=10,AC=6,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=8,
∵弦AE平分∠CAB,
∴$\frac{AC}{AB}$=$\frac{CG}{BE}$,
∴CG=3,BG=5,
∵∠CAE=∠EAB,∠ACB=∠AEB=90°,
∴△CAG∽△EAB,
∴$\frac{BE}{AE}$=$\frac{GC}{AC}$=$\frac{1}{2}$,
设BE=x,则AE=2x,
由勾股定理得,(2x)2+x2=100,
解得,x=2$\sqrt{5}$,
则AE=2x=4$\sqrt{5}$;
(2)连接OD,作OF⊥CD于F, 设AB交CD于点P,
设AB交CD于点P,
∵AM⊥CD,BN⊥CD,
∴AM∥BN,
∴$\frac{AP}{BP}$=$\frac{AM}{BN}$=$\frac{4}{3}$,又AB=10,
∴AP=$\frac{40}{7}$,BP=$\frac{30}{7}$,
则OP=$\frac{5}{7}$,
∵弦CD平分∠ACB,
∴$\frac{AC}{BC}$=$\frac{AP}{BP}$=$\frac{4}{3}$,
∴AC=8,
又∵∠CAM=45°,
∴AM=4$\sqrt{2}$,
∵$\frac{OF}{AM}$=$\frac{PO}{PA}$,
∴OF=$\frac{\sqrt{2}}{2}$,
∴DF=$\frac{7\sqrt{2}}{2}$,
∴CD=2DF=7$\sqrt{2}$.
点评 本题考查的是垂径定理、圆周角定理和勾股定理的应用,正确作出辅助线、灵活运用相关定理是解题的关键,注意相似三角形的判定和性质的应用.

 名校课堂系列答案
名校课堂系列答案 如图,A、B两点分别位于一个池塘的两端,为了测量A、B之间的距离,小天想了一个办法:在地上取一点C,使它可以直接到达A﹑B两点,连接AC、BC,在AC上取一点M,使AM=3MC,作MN∥AB交BC于点N,测得MN=38m,则A、B两点间的距离为( )
如图,A、B两点分别位于一个池塘的两端,为了测量A、B之间的距离,小天想了一个办法:在地上取一点C,使它可以直接到达A﹑B两点,连接AC、BC,在AC上取一点M,使AM=3MC,作MN∥AB交BC于点N,测得MN=38m,则A、B两点间的距离为( )| A. | 76m | B. | 95m | C. | 114m | D. | 152m |
| A. | $\frac{π}{9}$ | B. | -$\frac{π}{9}$ | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
| A. | 全等三角形的三条边相等,三个角也相等 | |
| B. | 判定两个三角形全等的条件中至少有一个是边 | |
| C. | 面积相等的两个图形是全等形 | |
| D. | 全等三角形的面积和周长都相等 |