题目内容
1．若a，b满足|a+5b-2|+（a+b-6）2=0，求代数式（a-3b）（a+2b）-（a+5b）（a+3b）的值．分析 根据非负数的性质，求得a，b的值，化简原式，再把a，b的值代入即可得出答案．
解答 解：∵|a+5b-2|+（a+b-6）2=0，
∴$\left\{\begin{array}{l}{a+5b-2=0}\\{a+b-6=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=7}\\{b=-1}\end{array}\right.$，
∴原式=a2+2ab-3ab-6b2-a2-3ab-5ab-15b2
=-9ab-21b2．
=-9×7×（-1）-21×（-1）2
=42．
点评 本题考查了整式的混合运算，以及非负数的性质，掌握多项式的乘法是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
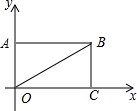如图，矩形ABCO，∠BOC=30°，OB=4，则点A的坐标为（0，2），点B的坐标为（2$\sqrt{3}$，2）．