题目内容
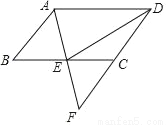
如图，在?ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．
（1）求证：AB=CF；
（2）连接DE，若AD=2AB，求证：DE⊥AF．
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由在?ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AB∥DF， ∴∠ABE=∠FCE， ∵E为BC中点， ∴BE=C...
三新快车金牌周周练系列答案甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞100．
（1）根据题意，填写下表（单位：元）；
累计购物 实际花费 | 130 | 290 | … | x |
在甲商场 | 127 |
| … |
|
在乙商场 | 126 |
| … |
|
（2）当x取何值时，小红在甲、乙两商场的实际花费相同？
（3）当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？
（1）在甲商场：100+（290﹣100）×0.9=271，100+（x﹣100）×0.9=0.9x+10；
在乙商场：50+（290﹣50）×0.95=278，50+（x﹣50）×0.95=0.95x+2.5；
（2）当x为150时，小红在甲、乙两商场的实际花费相同；
（3）当小红累计购物超过100元而不到150元时，在乙商场实际花费少；正好为150元时，两商场花费相同；大于1... 如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．
（1）证明见解析；（2）6．
【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；
（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．
试题解析：（1）∵D、G分别是AB、AC的中点，... 若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（ ）
A. 7 B. 10 C. 35 D. 70
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式，即可得出关于n的一元一次方程，解方程即可求出n的值，将其代入中即可得出结论．
【解析】
∵一个正n边形的每个内角为144°，
∴144n=180×（n﹣2），解得：n=10．
这个正n边形的所有对角线的条数是：==35．
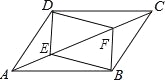
故选C． 如图，在?ABCD中，点E，F在对角线AC上，且AE=CF．求证：
（1）DE=BF；
（2）四边形DEBF是平行四边形．
详见解析.
【解析】
试题分析：（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD∥CB，AD=CB，
∴∠DAE=∠BCF，
在△ADE和△CBF中，
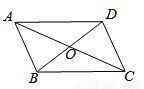
∴△AD... 如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件_________
（只添一个即可），使四边形ABCD是平行四边形
BO=DO
【解析】【解析】
∵AO=CO，BO=DO，∴四边形ABCD是平行四边形．故答案为：BO=DO． 如图，在?ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于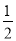
EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（ ）
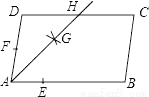
A. AG平分∠DAB B. AD=DH C. DH=BC D. CH=DH
D
【解析】试题分析：由角平分线的作法，依题意可知AG平分∠DAB，A正确；∠DAH＝∠BAH，又AB∥DC，所以∠BAH＝∠ADH，所以，∠DAH＝∠ADH，所以，AD＝DH，又AD＝BC，所以，DH＝BC，B、C正确，故答案选D. 如图，在四边形ABCD中，AB∥DC，E是AD中点，EF⊥BC于点F，BC=5，EF=3．
（1）若AB=DC，则四边形ABCD的面积S=__；
（2）若AB＞DC，则此时四边形ABCD的面积S′__S（用“＞”或“=”或“＜”填空）．
(1)15；（2）=．
【解析】试题分析：（1）∵AB=DC，AB∥DC，
∴四边形ABCD是平行四边形，
∴四边形ABCD的面积S=5×3=15，
（2）如图，连接EC，延长CD、BE交于点P，
∵E是AD中点，
∴AE=DE，
又∵AB∥CD，
∴∠ABE=∠P，∠A=∠PDE，
在△ABE和△DPE中，
∵，
∴△ABE≌△D... 今年，6月12日为端午节．在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况．请根据小丽提供的信息，解答小华和小明提出的问题．
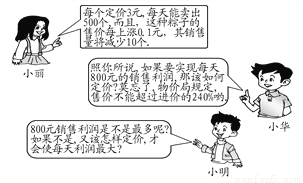
(1)当定价为4元时，能实现每天800元的销售利润(2)当定价为4.8元时，每天的销售利润最大．
【解析】试题分析：（1）小华的问题要用一元二次方程来解决，解答的关键是弄清：设实现每天800元利润的定价为x元/个时，每一个粽子的利润为（x-2）元，一共能卖（500-×10）个粽子，根据题意列方程得：（x-2)（500-×10）=800，解得x1=4,x2=6，还应根据实际问题确定两个值是否都...