题目内容
在△ABC中，∠A=∠B=∠C，AB=6，AD⊥BC，垂足为D，则BD的长为 ．
考点：等边三角形的性质
专题：
分析：直接根据等边三角形三线合一的性质进行解答即可．
解答：
解：如图所示，
∵∠A=∠B=∠C，
∴△ABC是等边三角形，
∴AB=BC=6，
∵AD⊥BC，
∴BD=CD=
BC=
×6=3．
故答案为：3．
解：如图所示，∵∠A=∠B=∠C，
∴△ABC是等边三角形，
∴AB=BC=6，
∵AD⊥BC，
∴BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：3．
点评：本题考查的是等边三角形的性质，熟知三条边都相等的三角形叫做等边三角形是解答此题的关键．
练习册系列答案
相关题目
写出下列的代数式中，错误的是（ ）
| A、x，y的平方差是：x2-y2 | ||||
B、甲数是a，甲数是乙数的
| ||||
| C、x的3倍与y的35%的和：3x+35%y | ||||
D、x除以y与3的和的平方：(
|
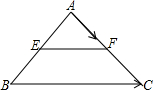已知：如图，EF是△ABC的中位线，设
已知二次函数y=x2+bx+c的图象经过点（4，3），（3，0）．
如图，AB为⊙O的直径，射线AP交⊙O于C点，∠PCO的平分线交⊙O于D点，过点D作DE⊥AP交AP于E点．
如图，在平行四边形ABCD中，E为CD上一点，联结AE、BD，且AE、BD交于点F，若DE：EC=2：3，则S△DEF：S△ABF=
如图，PA、PB是⊙O的切线，A、B分别为切点，PO交圆于点C，若∠APB=60°，PC=6，则AC的长为（ ）| A、4 | ||
B、2
| ||
C、2
| ||
D、3
|
如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=6