Question

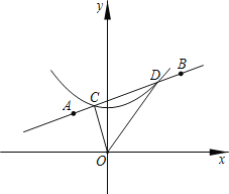
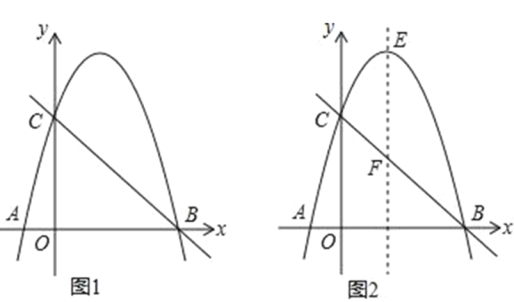
【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c（a＜0）经过点A（-1，0）、B（4，0）与y轴交于点C，tan∠ABC=．

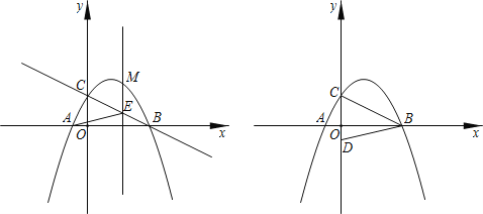
（1）求抛物线的解析式；

（2）点M在第一象限的抛物线上，ME平行y轴交直线BC于点E，连接AC、CE，当ME取值最大值时，求△ACE的面积．

（3）在y轴负半轴上取点D（0，-1），连接BD，在抛物线上是否存在点N，使∠BAN=∠ACO-∠OBD？若存在，请求出点N的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=-x2+x+2；（2）S△ACE=；（3）存在，N点的坐标为（，）或（，-）．

【解析】

（1）根据tan∠ABC=求出点C的坐标，再根据A，B，C的坐标求出解析式即可；

（2）先求出直线BC的解析式，设出M，E的坐标，求出ME的最大值，即可求出△ACE的面积；

（3）作C′（0，-2）与 C关于x轴对称，连接BC′，过点D作DE⊥BC′于点E，证明△AOC∽△COB，得到∠BAN=∠ACO-∠OBD=∠DBC′，得出tan∠DBC′=tan∠BAN=，再设N点坐标，根据tan∠BAN=，求出n的值，即可求出N点坐标.

（1）∵B（4，0），

∴OB=4，

∵tan∠ABC===，

∴OC=2，

∴C（0，2），

设y=a（x-1）（x-4），

把C（0，2）代入，得a=-，

∴抛物线的解析式为y=-（x-1）（x-4）=-x2+x+2；

（2）设直线BC的解析式为y=kx+2，

把B（4，0）代入，得k=-，

∴直线BC解析式为y=-x+2，

设M（m，-m2+m+2），

则E（m，-m+2），

∴ME=-m2+2m，

∴当m=2时，ME取得最大值2，

∴E（2，1），

∴S△ACE=S△ABC-S△ABE=×5×（2-1）=；

（3）作C′（0，-2）与 C关于x轴对称，连接BC′，过点D作DE⊥BC′于点E，

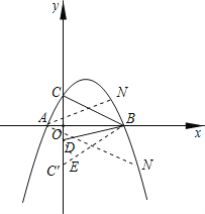
∴∠ABC=∠ABC′，

∵=，∠AOC=∠BOC=90°，

∴△AOC∽△COB，

∴∠ABC=∠ACO，

∴∠ABC′=∠ACO，

即∠BAN=∠ACO-∠OBD=∠DBC′，

由题意得DC′=1、DB=，BC′=2，

∵S△DBC′=，

∴DE=，

∴BE=，

∴tan∠DBC′=tan∠BAN=，

设N（n，-n2+n+2），且n＞0，

∴tan∠BAN===，

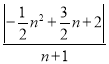①当2n+2=9×（-n2+n+2）时，n1=，n2=-1（舍去）；

②当2n+2=-9×（-n2+n+2）时，n1=，n2=-1（舍去）；

∴N点的坐标为（，）或（，-）．