题目内容
下列函数解析式中，表示是一次函数有_____个．
（1）y=5x+1，（2）y=kx+b，（3）y=3（x-1）-3x，（4）y=9，（5）
．
- A.1
- B.2
- C.3
- D.4
B
分析：根据一次函数的定义：一般地，形如y=kx+b（k≠0，k、b是常数）的函数，叫做一次函数；一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1．进行逐一分析即可．
解答：（1）y=5x+1是一次函数；
（2）y=kx+b，k=0时不是一次函数；
（3）y=3（x-1）-3x=3x-3-3x=-3，不是一次函数；
（4）y=9不是一次函数；
（5）y=4+
是一次函数；
故选：B．
点评：此题主要考查了一次函数定义，解题关键是掌握一次函数的定义条件：一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1．
分析：根据一次函数的定义：一般地，形如y=kx+b（k≠0，k、b是常数）的函数，叫做一次函数；一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1．进行逐一分析即可．
解答：（1）y=5x+1是一次函数；
（2）y=kx+b，k=0时不是一次函数；
（3）y=3（x-1）-3x=3x-3-3x=-3，不是一次函数；
（4）y=9不是一次函数；
（5）y=4+
是一次函数；故选：B．
点评：此题主要考查了一次函数定义，解题关键是掌握一次函数的定义条件：一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
图1是棱长为a的小正方体，图2、图3由这样的小正方体摆放而成．按照这样的方法继续摆放，由上而下分别叫第一层、第二层、…第n层，第n层的小正方体的个数为s．解答下列问题：
（1）按照要求填表：
（2）写出当n=10时，s= ；
（3）根据上表中的数据，把s作为纵坐标，n作为横坐标，在平面直角坐标系中描出相应的各点；
（4）合情猜想符合这图形的函数解析式，求出该函数的解析式，并验证这些点的坐标是否满足函数解析式．
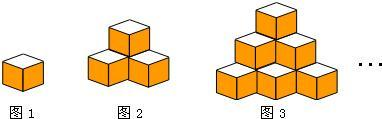
（1）按照要求填表：
| n | 1 | 2 | 3 | 4 | … |
| S | 1 | 3 | 6 | … |
（3）根据上表中的数据，把s作为纵坐标，n作为横坐标，在平面直角坐标系中描出相应的各点；
（4）合情猜想符合这图形的函数解析式，求出该函数的解析式，并验证这些点的坐标是否满足函数解析式．
李明因工作需要，每月要发送一定数量的手机短信，于是向同事老王和小张询问有关的费用标准．
老王说：“我平常发短信不多，我用拇指卡．”说完递给李明一张宣传单（见下表）．
小张说：“我发短信很多，用至尊卡更省钱，也获赠彩铃．”他画出至尊卡的费用y（元）与短信x（条）的函数关系图．
请解答下列问题：
（1）拇指卡的费用y（元）与短信x（条）的函数关系是 ；（温馨提示：费用=月租费+短信费）
（2）在图中画出（1）中的函数图象；
（3）求BC的函数解析式；
（4）请对以上两种收费标准进行分析，帮助李明理智选择一种实惠的短信服务；
（5）解释线段AB所表示的实际意义．
老王说：“我平常发短信不多，我用拇指卡．”说完递给李明一张宣传单（见下表）．
| 资费名称 | 月租费（元） | 单价（元/条） | 备注 |
| 拇指卡 | 8 | 0.06 | 赠送彩铃 |
小张说：“我发短信很多，用至尊卡更省钱，也获赠彩铃．”他画出至尊卡的费用y（元）与短信x（条）的函数关系图．请解答下列问题：
（1）拇指卡的费用y（元）与短信x（条）的函数关系是
（2）在图中画出（1）中的函数图象；
（3）求BC的函数解析式；
（4）请对以上两种收费标准进行分析，帮助李明理智选择一种实惠的短信服务；
（5）解释线段AB所表示的实际意义．
已知二次函数y=ax2+bx+c（a≠0）自变量x与函数值y之间满足下列数量关系：
（1）观察表中数据，当x=6时，y的值是 ；
（2）这个二次函数与x轴的交点坐标是 ；
（3）代数式
+
+（a+b+c）（a-b+c）的值是 ；
（4）若s、t是两个不相等的实数，当s≤x≤t时，二次函数y=ax2+bx+c（a≠0）有最小值0和最大值24，那么经过点（s+1，t+1）的反比例函数解析式是 ．
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 24 | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 |
（2）这个二次函数与x轴的交点坐标是
（3）代数式
-b+
| ||
| 2a |
-b-
| ||
| 2a |
（4）若s、t是两个不相等的实数，当s≤x≤t时，二次函数y=ax2+bx+c（a≠0）有最小值0和最大值24，那么经过点（s+1，t+1）的反比例函数解析式是
图1是棱长为a的小正方体，图2、图3由这样的小正方体摆放而成．按照这样的方法继续摆放，由上而下分别叫第一层、第二层、…第n层，第n层的小正方体的个数为s．解答下列问题：
（1）按照要求填表：
| n | 1 | 2 | 3 | 4 | … |
| S | 1 | 3 | 6 | … |
（3）根据上表中的数据，把s作为纵坐标，n作为横坐标，在平面直角坐标系中描出相应的各点；
（4）合情猜想符合这图形的函数解析式，求出该函数的解析式，并验证这些点的坐标是否满足函数解析式．
已知二次函数y=ax2+bx+c（a≠0）自变量x与函数值y之间满足下列数量关系：
（1）观察表中数据，当x=6时，y的值是______；
（2）这个二次函数与x轴的交点坐标是______；
（3）代数式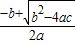
+
+（a+b+c）（a-b+c）的值是______；
（4）若s、t是两个不相等的实数，当s≤x≤t时，二次函数y=ax2+bx+c（a≠0）有最小值0和最大值24，那么经过点（s+1，t+1）的反比例函数解析式是______．
| x | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 | |
| y | 24 | 15 | 8 | 3 | -1 | 3 | 8 | 15 |
（2）这个二次函数与x轴的交点坐标是______；
（3）代数式
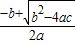++（a+b+c）（a-b+c）的值是______；（4）若s、t是两个不相等的实数，当s≤x≤t时，二次函数y=ax2+bx+c（a≠0）有最小值0和最大值24，那么经过点（s+1，t+1）的反比例函数解析式是______．