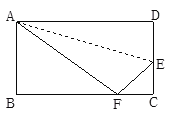
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨ…ζ≤ζ![]() ΝΫ÷÷…η±ΗΘ§“―÷ΣΟΩΧ®
ΝΫ÷÷…η±ΗΘ§“―÷ΣΟΩΧ®![]() ÷÷…η±ΗΒΡ≥…±Ψ «
÷÷…η±ΗΒΡ≥…±Ψ «![]() ÷÷…η±ΗΒΡ1Θ°5±ΕΘ§ΙΪΥΨ»τΆΕ»κ6Άρ‘Σ…ζ≤ζ
÷÷…η±ΗΒΡ1Θ°5±ΕΘ§ΙΪΥΨ»τΆΕ»κ6Άρ‘Σ…ζ≤ζ![]() ÷÷…η±ΗΘ§ΆΕ»Υ15Άρ‘Σ…ζ≤ζ
÷÷…η±ΗΘ§ΆΕ»Υ15Άρ‘Σ…ζ≤ζ![]() ÷÷…η±ΗΘ§‘ρΩ……ζ≤ζΝΫ÷÷…η±ΗΙ≤40Χ®Θ°«κΫβ¥πœ¬Ν–Έ ΧβΘΚ
÷÷…η±ΗΘ§‘ρΩ……ζ≤ζΝΫ÷÷…η±ΗΙ≤40Χ®Θ°«κΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©![]() ΝΫ÷÷…η±ΗΟΩΧ®ΒΡ≥…±ΨΖ÷±π «Εύ…ΌΆρ‘ΣΘΩ
ΝΫ÷÷…η±ΗΟΩΧ®ΒΡ≥…±ΨΖ÷±π «Εύ…ΌΆρ‘ΣΘΩ
Θ®2Θ©»τ![]() ΝΫ÷÷…η±ΗΟΩΧ®ΒΡ έΦέΖ÷±π «5000‘ΣΓΔ9000‘ΣΘ§ΙΪΥΨΨωΕ®…ζ≤ζΝΫ÷÷…η±ΗΙ≤50Χ®Θ§«“Τδ÷–
ΝΫ÷÷…η±ΗΟΩΧ®ΒΡ έΦέΖ÷±π «5000‘ΣΓΔ9000‘ΣΘ§ΙΪΥΨΨωΕ®…ζ≤ζΝΫ÷÷…η±ΗΙ≤50Χ®Θ§«“Τδ÷–![]() ÷÷…η±Η÷Ν…Ό…ζ≤ζ10Χ®Θ§ΦΤΜ°œζ έΚσΜώάϊ≤ΜΒΆ”Ύ12Άρ‘ΣΘ§«κΈ ≤…”ΟΡΡ÷÷…ζ≤ζΖΫΑΗΙΪΥΨΥυΜώάϊ»σΉν¥σΘΩ≤Δ«σ≥ωΉν¥σάϊ»σΘ°
÷÷…η±Η÷Ν…Ό…ζ≤ζ10Χ®Θ§ΦΤΜ°œζ έΚσΜώάϊ≤ΜΒΆ”Ύ12Άρ‘ΣΘ§«κΈ ≤…”ΟΡΡ÷÷…ζ≤ζΖΫΑΗΙΪΥΨΥυΜώάϊ»σΉν¥σΘΩ≤Δ«σ≥ωΉν¥σάϊ»σΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0.4Άρ‘ΣΘ§
÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0.4Άρ‘ΣΘ§![]() ÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0.6Άρ‘ΣΘΜΘ®2Θ©ΙΪΥΨ…ζ≤ζ10Χ®
÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0.6Άρ‘ΣΘΜΘ®2Θ©ΙΪΥΨ…ζ≤ζ10Χ®![]() ÷÷…η±ΗΘ§40Χ®
÷÷…η±ΗΘ§40Χ®![]() ÷÷…η±Η ±ΥυΜώάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ130000‘ΣΘ°
÷÷…η±Η ±ΥυΜώάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ130000‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηA÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «xΆρ‘ΣΘ§B÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «1.5xΆρ‘ΣΘ°ΗυΨίΓΑ ΐΝΩΘΫΉήΦέΓ¬ΒΞΦέΓ±ΫαΚœΓΑΆΕ»κΆΕ»κ1.5Άρ‘Σ…ζ≤ζA÷÷…η±ΗΘ§3.75Άρ‘Σ…ζ≤ζB÷÷…η±ΗΘ§‘ρΩ……ζ≤ζΝΫ÷÷…η±ΗΙ≤10Χ®Γ±Θ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎxΒΡΖ÷ ΫΖΫ≥ΧΘ§Ϋβ÷°Ψ≠Φλ―ιΚσΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©…ηΙΪΥΨΜώΒΟάϊ»σΈΣW‘ΣΘ§A÷÷…η±Η…ζ≤ζaΧ®Θ§‘ρB÷÷…η±Η…ζ≤ζΘ®50©¹aΘ©Χ®Θ°ΗυΨίœζ έΚσΜώάϊ≤ΜΒΆ”Ύ12Άρ‘Σ«“A÷÷…η±Η÷Ν…Ό…ζ≤ζ10Χ®Θ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎaΒΡ“Μ‘Σ“Μ¥Έ≤ΜΒ» ΫΉιΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωaΒΡ»Γ÷ΒΖΕΈßΘ§ΗυΨίΧβ“βΒΟ≥ωW”κaΒΡΚ· ΐΙΊœΒ ΫΘ§‘ΌΗυΨί“Μ¥ΈΚ· ΐΒΡ–‘÷ Ϋβ¥πΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©…η![]() ÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «
÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «![]() Άρ‘ΣΘ§‘ρ
Άρ‘ΣΘ§‘ρ![]() ÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «
÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «![]() Άρ‘ΣΘ°
Άρ‘ΣΘ°
ΗυΨίΧβ“βΘ§ΒΟ![]() Θ§
Θ§
ΫβΒΟ![]() Θ°
Θ°
Ψ≠Φλ―ι![]() «Ζ÷ ΫΖΫ≥ΧΒΡΫβΘ§
«Ζ÷ ΫΖΫ≥ΧΒΡΫβΘ§
‘ρ![]() Θ°
Θ°
¥πΘΚ![]() ÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0Θ°4Άρ‘ΣΘ§
÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0Θ°4Άρ‘ΣΘ§![]() ÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0Θ°6Άρ‘ΣΘ°
÷÷…η±ΗΟΩΧ®ΒΡ≥…±Ψ «0Θ°6Άρ‘ΣΘ°
Θ®2Θ©…ηΙΪΥΨΜώΒΟΒΡάϊ»σΈΣ![]() ‘ΣΘ§…ζ≤ζ
‘ΣΘ§…ζ≤ζ![]() ÷÷…η±Η
÷÷…η±Η![]() Χ®Θ§‘ρ…ζ≤ζ
Χ®Θ§‘ρ…ζ≤ζ![]() ÷÷…η±Η
÷÷…η±Η![]() Χ®Θ°
Χ®Θ°
ΗυΗυΨίΧβ“βΘ§ΒΟ![]() Θ§
Θ§
ΫβΒΟ![]() Θ°
Θ°
![]() Θ§
Θ§![]() Θ°
Θ°
![]() Θ§Φ¥
Θ§Φ¥![]() Θ°
Θ°
![]() Θ§
Θ§
![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχΦθ–ΓΘ§
ΒΡ‘ω¥σΕχΦθ–ΓΘ§
![]() Β±
Β±![]() ±Θ§ΥυΜώάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ
±Θ§ΥυΜώάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ![]() Θ®‘ΣΘ©Θ°
Θ®‘ΣΘ©Θ°
¥πΘΚΙΪΥΨ…ζ≤ζ10Χ®![]() ÷÷…η±ΗΘ§40Χ®
÷÷…η±ΗΘ§40Χ®![]() ÷÷…η±Η ±ΥυΜώάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ130000‘ΣΘ°
÷÷…η±Η ±ΥυΜώάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ130000‘ΣΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ