Question

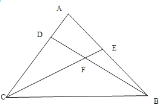
【题目】在△ABC中，∠ACB=60°，CE为△ABC的角平分线，AC边上的高BD与CE所在的直线交于点F，若∠ABD:∠ACF=2:3，则∠BEC的度数为_____.

Answer 1

【答案】100°；

【解析】

根据直角三角形的性质得∠BDC=90°，根据角平分线的性质得∠ECB=∠ECA =30°，再结合题意可以得到答案.

因为AC边上的高BD与CE所在的直线交于点F，

所以∠BDC=90°，

由∠ACB=60°，三角形内角和为180°，

可得∠DBC=180°-90°-60°=30°，

因为CE为△ABC的角平分线，

所以∠ECB=∠ECA =30°，

由∠ABD:∠ACF=2:3，且∠ECA=∠ACF =30°，

则∠ABD=20°，

则∠ABC=∠ABD+∠DBC=50°，

所以∠BEC=180°-∠DBC-∠ECB=100°，

故答案为100°.