ĢāÄæÄŚČŻ
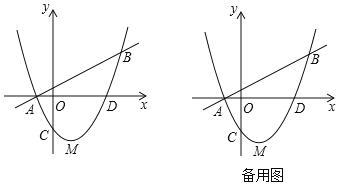
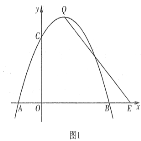
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µć![]() ĪŖ×ų±źŌµć£¬Å×ĪļĻß
ĪŖ×ų±źŌµć£¬Å×ĪļĻß![]() ½»
½»![]() ÖįÓŚ
ÖįÓŚ![]() Į½µć£¬½»
Į½µć£¬½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ¹żÅ×ĪļĻߵĶ„µć
¹żÅ×ĪļĻߵĶ„µć![]() £¬½»
£¬½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬ĒŅ
£¬ĒŅ![]() £®
£®
£Ø1£©Ēó![]() ŗĶ
ŗĶ![]() µÄÖµ£»
掙术
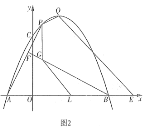
£Ø2£©ČēĶ¼2£¬µć![]() ŌŚµć
ŌŚµć![]() ŗĶµć
ŗĶµć![]() Ö®¼äµÄÅ×ĪļĻßÉĻ£¬Į¬½Ó
Ö®¼äµÄÅ×ĪļĻßÉĻ£¬Į¬½Ó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() Öį½»
Öį½»![]() ÓŚµć
ÓŚµć![]() £¬µć
£¬µć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÓŅ²ąµÄ
ÓŅ²ąµÄ![]() ÖįÉĻ£¬Į¬½Ó
ÖįÉĻ£¬Į¬½Ó![]() £¬ĒŅ
£¬ĒŅ![]() £¬Éčµć
£¬Éčµć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬Ļ߶Ī
£¬Ļ߶Ī![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
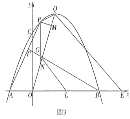
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Į¬½Ó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬ŃÓ³¤
£¬ŃÓ³¤![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬Į¬½Ó
ÉĻ£¬Į¬½Ó![]() £¬Čō
£¬Čō![]() £¬Ēó
£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
”¾“š°ø”æ£Ø1£©![]() £¬
£¬![]() £»£Ø2£©
£»£Ø2£©![]() £»£Ø3£©
£»£Ø3£©![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©Įī![]() £¬Ēó³ö
£¬Ēó³ö![]() £¬
£¬![]() £¬ÉčÅ×ĪļĻ߶Ō³ĘÖį½»
£¬ÉčÅ×ĪļĻ߶Ō³ĘÖį½»![]() ÖįÓŚ
ÖįÓŚ![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬![]() £¬Ēó³ö
£¬Ēó³ö![]() £¬µĆµ½
£¬µĆµ½![]() £¬“śČė
£¬“śČė![]() £¬Ēó³öh£¬µĆµ½
£¬Ēó³öh£¬µĆµ½![]() £¬“śČė
£¬“śČė![]() Ēó³ök£»
Ēó³ök£»
£Ø2£©ŃÓ³¤![]() ½»
½»![]() ÖįÓŚ
ÖįÓŚ![]() £¬Éč
£¬Éč![]() £¬µĆ
£¬µĆ![]() £¬øł¾ŻÕżĒŠ¶ØŅåæɵĆ
£¬øł¾ŻÕżĒŠ¶ØŅåæɵĆ![]() £¬¼“
£¬¼“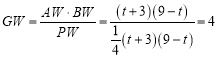 £¬ÓÉ
£¬ÓÉ![]() £¬Ēó³ö
£¬Ēó³ö![]() £¬“Ó¶ųĒó³ö
£¬“Ó¶ųĒó³ö![]() £»
£»
£Ø3£©»ł±¾Ė¼Ā·£ŗ¹¹ŌģÖ±½ĒČż½ĒŠĪ£¬ĄūÓĆÕżĒŠ¶ØŅåĮŠ³öµČŹ½£®¼“£ŗŃÓ³¤![]() ŗĶ
ŗĶ![]() ½»ÓŚµć
½»ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬ŌŚ
£¬ŌŚ![]() ÉĻČ”µć
ÉĻČ”µć![]() £¬Ź¹
£¬Ź¹![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £®øł¾ŻĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄżæÉĒó³ö
£®øł¾ŻĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄżæÉĒó³ö![]() £¬øł¾ŻÕżĒŠ¶ØŅåµĆ
£¬øł¾ŻÕżĒŠ¶ØŅåµĆ![]() £¬¼“
£¬¼“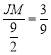 £¬Ēó³ö
£¬Ēó³ö![]() £¬øł¾Ż
£¬øł¾Ż![]() £¬Ēó³ö
£¬Ēó³ö![]() £¬PN£¬µĆµ½
£¬PN£¬µĆµ½![]() £¬“śČė½āĪöŹ½Ēó³öt£¬ŌŁµĆµ½WE£¬NT£¬TK£»Éč
£¬“śČė½āĪöŹ½Ēó³öt£¬ŌŁµĆµ½WE£¬NT£¬TK£»Éč![]() £¬Ēó³ö
£¬Ēó³ö![]() £¬øł¾ŻÖ±½ĒČż½ĒŠĪŠŌÖŹµĆµ½
£¬øł¾ŻÖ±½ĒČż½ĒŠĪŠŌÖŹµĆµ½![]() £¬¹Ź
£¬¹Ź![]() £¬
£¬![]() £¬¼“
£¬¼“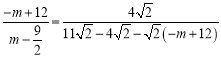 £®
£®
½ā£ŗ£Ø1£©µ±![]() Ź±£¬
Ź±£¬![]() £¬½āµĆ£¬
£¬½āµĆ£¬![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą![]() £¬
£¬
ÉčÅ×ĪļĻ߶Ō³ĘÖį½»![]() ÖįÓŚ
ÖįÓŚ![]() £¬
£¬
”ą![]() £¬Éč
£¬Éč![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą![]() £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() £¬“śČė
£¬“śČė![]() £¬
£¬
¼“![]() £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() “śČĖ
“śČĖ![]() £¬¼“
£¬¼“![]() £¬
£¬
”ą![]() £»
£»
£Ø2£©ŃÓ³¤![]() ½»
½»![]() ÖįÓŚ
ÖįÓŚ![]() £¬
£¬
Éč![]() £¬”ą
£¬”ą![]() £¬
£¬
”ß![]() £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą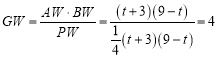 £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą![]() £»
£»
£Ø3£©ŃÓ³¤![]() ŗĶ
ŗĶ![]() ½»ÓŚµć
½»ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬ŌŚ
£¬ŌŚ![]() ÉĻČ”µć
ÉĻČ”µć![]() £¬Ź¹
£¬Ź¹![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬¼“
£¬¼“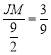 £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() £¬½āµĆ£¬
£¬½āµĆ£¬![]() »ņ
»ņ![]() £ØÉį£©£¬
£ØÉį£©£¬
”ą![]() £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą![]() £¬
£¬
Éč![]() £¬
£¬
”ą![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
øł¾ŻÖ±½ĒČż½ĒŠĪŠŌÖŹµĆ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
¼“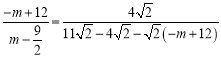 £¬
£¬
½āµĆ![]() »ņ
»ņ![]() £¬
£¬
”ą![]() »ņ
»ņ![]() £®
£®