题目内容
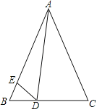
【题目】如图已知直线![]() 与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣
与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣![]() ),交x轴正半轴于D点,抛物线的顶点为M.
),交x轴正半轴于D点,抛物线的顶点为M.
(1)求抛物线的解析式;
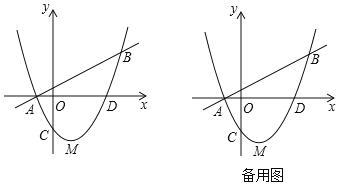
(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;
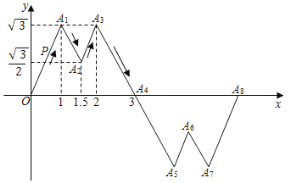
(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,P(
,P(![]() ,
,![]() );(3)N(3,0)或N(2+
);(3)N(3,0)或N(2+![]() ,1+
,1+![]() )或N(5,6)或N(
)或N(5,6)或N(![]() ,1﹣
,1﹣![]() ).
).
【解析】
(1)将点![]() 代入
代入![]() ,求出
,求出![]() ,将点
,将点![]() 代入
代入![]() ,即可求函数解析式; (2)如图,过
,即可求函数解析式; (2)如图,过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,求出
,求出![]() 的解析式,设
的解析式,设![]() ,表示
,表示![]() 点坐标,表示
点坐标,表示![]() 长度,利用
长度,利用![]() ,建立二次函数模型,利用二次函数的性质求最值即可, (3)可证明△MAD是等腰直角三角形,由△QMN与△MAD相似,则△QMN是等腰直角三角形,设
,建立二次函数模型,利用二次函数的性质求最值即可, (3)可证明△MAD是等腰直角三角形,由△QMN与△MAD相似,则△QMN是等腰直角三角形,设![]() ①当MQ⊥QN时,N(3,0); ②当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,由
①当MQ⊥QN时,N(3,0); ②当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,由![]() (AAS),建立方程求解; ③当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点
(AAS),建立方程求解; ③当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点![]() 作
作![]() R∥x轴,与过M点的垂线分别交于点S、R;可证△MQR≌△QNS(AAS),建立方程求解; ④当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;可证△MNR≌△NQS(AAS),建立方程求解.
R∥x轴,与过M点的垂线分别交于点S、R;可证△MQR≌△QNS(AAS),建立方程求解; ④当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;可证△MNR≌△NQS(AAS),建立方程求解.
解:(1)将点![]() 代入
代入![]() ,∴
,∴![]() ,
,
将点![]() 代入
代入![]() ,
,
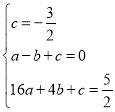 解得:
解得: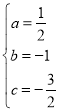 ,
,
∴函数解析式为![]() ;
;
(2)如图,过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,设
,设![]() 为
为![]() ,
,
因为:![]() 所以:
所以:
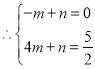 ,解得:
,解得: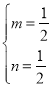 ,
,
所以直线AB为:![]() ,设
,设![]() ,则
,则![]() ,
,
所以:![]() ,
,
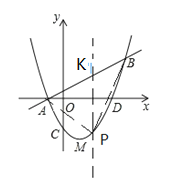
所以:![]()
![]() ,
,
当![]() ,
,![]() ,
,
此时:![]() .
.
(3)∵![]() ,
,
∴![]() ,
,
∴△MAD是等腰直角三角形.
∵△QMN与△MAD相似,∴△QMN是等腰直角三角形,
设![]()
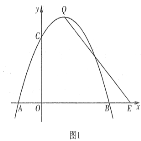
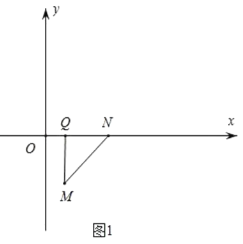
①如图1,当MQ⊥QN时,此时![]() 与
与![]() 重合,N(3,0);
重合,N(3,0);
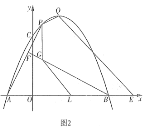
②如图2,当QN⊥MN时,过点N作NR⊥x轴于![]() ,过点M作MS⊥RN交于点S.
,过点M作MS⊥RN交于点S.
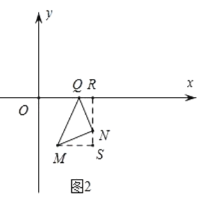
∵QN=MN,∠QNM=90°,∴![]() (AAS),
(AAS),![]()
∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
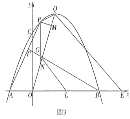
③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点![]() 作
作![]() R∥x轴,与过
R∥x轴,与过![]() 点的垂线分别交于点S、R;
点的垂线分别交于点S、R;
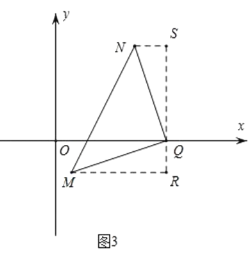
∵QN=MQ,∠MQN=90°,∴△MQR≌△QNS(AAS),![]() ,
,
![]() ,∴
,∴![]() ,∴t=5,(舍去负根)∴N(5,6);
,∴t=5,(舍去负根)∴N(5,6);
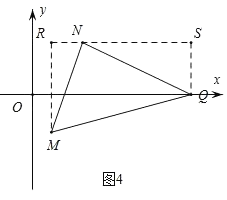
④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,
过点N作x轴的平行线,与两垂线交于点R、S;
∵QN=MN,∠MNQ=90°,∴△MNR≌△NQS(AAS),∴SQ=RN,
∴![]() ,∴
,∴![]() .
.
![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
综上所述:![]() 或
或![]() 或N(5,6)或
或N(5,6)或![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.