Question

已知，如图,抛物线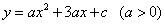与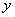轴交于点C，与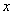轴交于A，B两点，点A在点B左侧．点B的坐标为(1,0)，OC＝3OB.

(1)求抛物线的解析式；

(2)若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；

(3)若点E在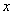轴上，点P在抛物线上．是否存在以A，C，E，P为顶点且以AC为一边的平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．

 

                             

Answer 1

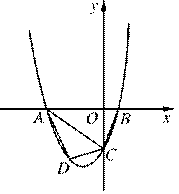
解：(1)∵OC＝3OB，B(1,0)，∴C(0，－3)．

把点B，C的坐标代入y＝ax²＋3ax＋c，得

解得

∴y＝x²＋x－3.                   ......................2分                 

(2)如图，过点D作DM∥y轴分别交线段AC和x轴于点M，N.

S_{四边形ABCD}＝S_△ABC＋S_△ACD

＝＋×DM×(AN＋ON)

＝＋2DM，

∵A(－4,0)，C(0，－3)，

设直线AC的解析式为y＝kx＋b，

代入，求得y＝－x－3.   ..................................4分

令D，M，

DM＝－x－3－

＝－(x＋2)²＋3

∵－<0，∴开口向下

    当x＝－2时，DM有最大值3.

此时四边形ABCD面积有最大值为.        ......................6分