题目内容
8.在$\root{3}{2}$,$\frac{1}{4}$,$\sqrt{7}$,π,-$\frac{5}{2}$,$\sqrt{\frac{4}{9}}$,$-\sqrt{5}$,0,-$\root{3}{8}$,0.3737737773…(相邻两个3之间的7的个数逐次加1)中,无理数有( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:$\root{3}{2}$,$\sqrt{7}$,π,$-\sqrt{5}$,0.3737737773…(相邻两个3之间的7的个数逐次加1)是无理数,
故选:D.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
相关题目
3. 如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )
如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )
 如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )
如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )| A. | 100° | B. | 80° | C. | 60° | D. | 40° |
20.点A(-1,2)绕坐标原点O逆时针方向旋转90°得到的点A'的坐标是( )
| A. | (-2,-1) | B. | (2,-1) | C. | (1,-2) | D. | (2,1) |

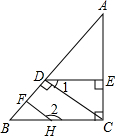 已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC.
已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC.