题目内容
 已知双曲线
已知双曲线 经过△AEO的顶点A,且AE=AO=5,tan∠AOE=
经过△AEO的顶点A,且AE=AO=5,tan∠AOE= ,直线y=kx+b与双曲线
,直线y=kx+b与双曲线 相交于A,F两点,且F点的坐标为(6,n)
相交于A,F两点,且F点的坐标为(6,n)
(1)求出反比例函数与一次函数的解析式;
(2)连接EF,求△AEF的面积.
解:(1)作AB⊥OE于E点,如图,
∵AO=AE,
∴OB=EB,
在RtAOB中
∵tan∠AOB=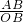 =
= ,
,
设AB=4x,则OB=3x,
∴OA=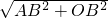 =5x,
=5x,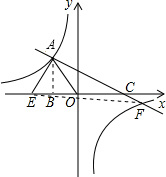
而AO=5,
∴x=1,
∴AB=4,OB=3,
∴A(-3,4),
把A(-3,4)代入y= 得m=-3×4=-12,
得m=-3×4=-12,
∴反比例函数的解析式为:y=- ,
,
把F(6,n)代入y=- 得6n=-12,解得n=-2,
得6n=-12,解得n=-2,
∴F点坐标为(6,-2),
把A(-3,4)、F(6,-2)代入y=kx+b得
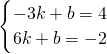 ,解得
,解得 ,
,
故一次函数的解析式为:y=-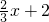 ;
;
(2)如图,C点坐标为(3,0),E点坐标为(-6,0),
S△AEF=S△AEC+S△FEC= ×9×4+
×9×4+ ×9×2=18+9=27.
×9×2=18+9=27.
分析:(1)作AB⊥OE于E点,根据等腰三角形的性质得OB=EB,利用正切的定义得tan∠AOB=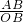 =
= ,设AB=4x,则OB=3x,根据勾股定理得OA=5x,则x=1,于是AB=4,OB=3,
,设AB=4x,则OB=3x,根据勾股定理得OA=5x,则x=1,于是AB=4,OB=3,
得到A(-3,4),把它代入反比例函数解析式求出k,接着确定F点坐标,然后利用待定系数法确定一次函数的解析式;
(2)先求出一次函数与x轴的交点坐标C(3,0),再根据B点坐标确定E点坐标,然后利用S△AEF=S△AEC+S△FEC进行计算.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数的解析式.也考查了待定系数法求函数的解析式、等腰三角形的性质以及三角形的面积公式.
∵AO=AE,
∴OB=EB,
在RtAOB中
∵tan∠AOB=
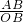 =
= ,
,设AB=4x,则OB=3x,
∴OA=
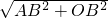 =5x,
=5x,
而AO=5,
∴x=1,
∴AB=4,OB=3,
∴A(-3,4),
把A(-3,4)代入y=
 得m=-3×4=-12,
得m=-3×4=-12,∴反比例函数的解析式为:y=-
 ,
,把F(6,n)代入y=-
 得6n=-12,解得n=-2,
得6n=-12,解得n=-2,∴F点坐标为(6,-2),
把A(-3,4)、F(6,-2)代入y=kx+b得
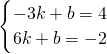 ,解得
,解得 ,
,故一次函数的解析式为:y=-
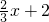 ;
;(2)如图,C点坐标为(3,0),E点坐标为(-6,0),
S△AEF=S△AEC+S△FEC=
 ×9×4+
×9×4+ ×9×2=18+9=27.
×9×2=18+9=27.分析:(1)作AB⊥OE于E点,根据等腰三角形的性质得OB=EB,利用正切的定义得tan∠AOB=
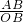 =
= ,设AB=4x,则OB=3x,根据勾股定理得OA=5x,则x=1,于是AB=4,OB=3,
,设AB=4x,则OB=3x,根据勾股定理得OA=5x,则x=1,于是AB=4,OB=3,得到A(-3,4),把它代入反比例函数解析式求出k,接着确定F点坐标,然后利用待定系数法确定一次函数的解析式;
(2)先求出一次函数与x轴的交点坐标C(3,0),再根据B点坐标确定E点坐标,然后利用S△AEF=S△AEC+S△FEC进行计算.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数的解析式.也考查了待定系数法求函数的解析式、等腰三角形的性质以及三角形的面积公式.

练习册系列答案
相关题目
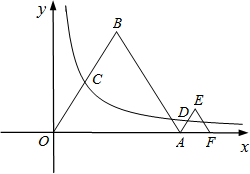 (2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
(2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=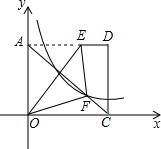 如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=
如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y= 经过△AEO的顶点A,且AE=AO=5,
经过△AEO的顶点A,且AE=AO=5, ,直线
,直线 与双曲线
与双曲线 )
)
 经过△AEO的顶点A,且AE=AO=5,
经过△AEO的顶点A,且AE=AO=5, ,直线
,直线 与双曲线
与双曲线 )
)