题目内容
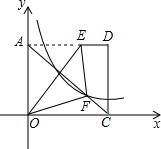 如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=
如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=| k |
| x |
80
| ||
| 81 |
80
| ||
| 81 |
分析:首先过点F作FN⊥CO于点N,过点F作FS⊥AD于点S,得出△OFN∽△FES,进而得出F点横坐标,再利用勾股定理得出FN的值,即可得出F点坐标,进而得出k的值.
解答: 解:过点F作FN⊥CO于点N,过点F作FS⊥AD于点S,
解:过点F作FN⊥CO于点N,过点F作FS⊥AD于点S,
∵将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,沿着OE所在直线对折,
点A恰好落在对角线AC上的F点处,AE=4,OC=5,
∴AE=EF=4,
设F点横坐标为x,设AO=y,
则ON=x,SE=x-4,FO=y,
∵FN∥AO,
∴
=
,
∴
=
,
则FN=
,
∴∠OFE=∠OAE=90°,
∴∠OFN+∠EFS=90°,
∠FON+∠OFN=90°,
∴∠FON=∠SFE,
∵∠ONF=∠FSE=90°,
∴△OFN∽△FES,
∴
=
,
∴
=
,
解得:x=
,
∴NC=5-
=
,
∴
=
=
=
,
∴FN=
y,
∴y2=(
y)2+(
)2,
解得:y1=2
,y2=-2
(不合题意舍去),
∴FN=
×2
=
,
∴F点坐标为:(
,
),
∴k=
×
=
.
故答案为:
.
 解:过点F作FN⊥CO于点N,过点F作FS⊥AD于点S,
解:过点F作FN⊥CO于点N,过点F作FS⊥AD于点S,∵将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,沿着OE所在直线对折,
点A恰好落在对角线AC上的F点处,AE=4,OC=5,
∴AE=EF=4,
设F点横坐标为x,设AO=y,
则ON=x,SE=x-4,FO=y,
∵FN∥AO,
∴
| FN |
| NC |
| AO |
| CO |
∴
| FN |
| 5-x |
| y |
| 5 |
则FN=
| y(5-x) |
| 5 |
∴∠OFE=∠OAE=90°,
∴∠OFN+∠EFS=90°,
∠FON+∠OFN=90°,
∴∠FON=∠SFE,
∵∠ONF=∠FSE=90°,
∴△OFN∽△FES,
∴
| FN |
| ES |
| FO |
| EF |
∴
| ||
| x-4 |
| y |
| 4 |
解得:x=
| 40 |
| 9 |
∴NC=5-
| 40 |
| 9 |
| 5 |
| 9 |
∴
| NC |
| CO |
| FN |
| AO |
| ||
| 5 |
| 1 |
| 9 |
∴FN=
| 1 |
| 9 |
∴y2=(
| 1 |
| 9 |
| 40 |
| 9 |
解得:y1=2
| 5 |
| 5 |
∴FN=
| 1 |
| 9 |
| 5 |
2
| ||
| 9 |
∴F点坐标为:(
| 40 |
| 9 |
2
| ||
| 9 |
∴k=
| 40 |
| 9 |
2
| ||
| 9 |
80
| ||
| 81 |
故答案为:
80
| ||
| 81 |
点评:此题主要考查了反比例函数综合以及相似三角形的性质、勾股定理等知识,根据已知得出F点横坐标是解题关键.

练习册系列答案
相关题目
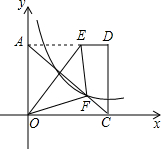 如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=
如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y= 经过点F,则k=________.
经过点F,则k=________.