题目内容
 如图,在5×5的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.(1)画线段AC,使它的另一个端点C落在格点(即小正方形的顶点)上,且长度为3
| 2 |
(2)以线段AC为对角线,画凸四边形ABCD,使四边形ABCD既是中心对称图形又是轴对称图形,顶点都在格点上,且边长是无理数;
(3)求(2)中四边形ABCD的周长和面积.
考点:勾股定理,利用轴对称设计图案,利用旋转设计图案
专题:
分析:(1)根据勾股定理,边长为3的正方形的对角线的长即为3
,然后确定出点C的位置即可;
(2)根据轴对称和中心对称的性质,四边形ABCD是菱形即可;
(3)利用勾股定理求出AB,再求出BD,然后根据菱形的周长和面积公式分别列式计算即可得解.
| 2 |
(2)根据轴对称和中心对称的性质,四边形ABCD是菱形即可;
(3)利用勾股定理求出AB,再求出BD,然后根据菱形的周长和面积公式分别列式计算即可得解.
解答: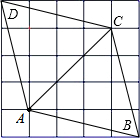 解:(1)线段AC如图所示;
解:(1)线段AC如图所示;
(2)四边形ABCD如图所示;
(3)由勾股定理得,AB=
=
,
BD=
=5
,
所以,四边形ABCD的周长=4
,
面积=3
×5
=30.
 解:(1)线段AC如图所示;
解:(1)线段AC如图所示;(2)四边形ABCD如图所示;
(3)由勾股定理得,AB=
| 42+12 |
| 17 |
BD=
| 52+52 |
| 2 |
所以,四边形ABCD的周长=4
| 17 |
面积=3
| 2 |
| 2 |
点评:本题考查了勾股定理,利用轴对称和旋转设计图案,熟练掌握网格结构以及菱形的性质的解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

