题目内容
6.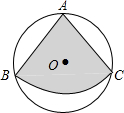 如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$米.
如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$米.
分析 圆的半径为1,那么过圆心向AC引垂线,利用相应的三角函数可得AC的一半的长度,进而求得AC的长度,利用弧长公式可求得弧BC的长度,圆锥的底面圆的半径=圆锥的弧长÷2π.
解答  解:作OD⊥AC于点D,连接OA,
解:作OD⊥AC于点D,连接OA,
∴∠OAD=45°,AC=2AD,
∴AC=2(OA×cos45°)=$\sqrt{2}$
∴$\frac{90π×\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π
∴圆锥的底面圆的半径=$\frac{\sqrt{2}}{2}$π÷(2π)=$\frac{\sqrt{2}}{4}$.
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16.若一个等腰三角形的两边长分别是2和5,则它的周长为( )
| A. | 12 | B. | 9 | C. | 12或9 | D. | 9或7 |
17.若(x+2)(x-1)=x2+mx+n,则m+n=( )
| A. | 1 | B. | -2 | C. | -1 | D. | 2 |
14. 如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧$\widehat{AMB}$上一点,则∠APB的度数为( )
如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧$\widehat{AMB}$上一点,则∠APB的度数为( )
 如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧$\widehat{AMB}$上一点,则∠APB的度数为( )
如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧$\widehat{AMB}$上一点,则∠APB的度数为( )| A. | 45° | B. | 30° | C. | 75° | D. | 60° |
11.近十天每天平均气温(℃)统计如下:24,23,22,24,24,27,30,31,30,29.关于这10个数据下列说法不正确的是( )
| A. | 众数是24 | B. | 中位数是26 | C. | 平均数是26.4 | D. | 极差是9 |
18.计算:(-$\frac{2}{3}$)0=( )
| A. | 1 | B. | -$\frac{3}{2}$ | C. | 0 | D. | $\frac{2}{3}$ |
 如图,某渔船在小岛O南偏东75°方向的B处遇险,在小岛O南偏西45°方向A处巡航的中国渔政船接到求救信号后立刻前往救援,此时,中国渔政船与小岛O相距8海里,渔船在中国渔政船的正东方向上.
如图,某渔船在小岛O南偏东75°方向的B处遇险,在小岛O南偏西45°方向A处巡航的中国渔政船接到求救信号后立刻前往救援,此时,中国渔政船与小岛O相距8海里,渔船在中国渔政船的正东方向上.
 要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.