题目内容
6.引入:在直角三角形中,已知任意两边长就能求出第三边,也可以已知一边和一个锐角,利用直角三角形中已知锐角的大小得出三边的比例关系,求出剩余两边的大小,这类内容称为解直角三角形.如图,在图①中,三边a:b:c=1:$\sqrt{3}$:2,在图②中,三边a:b:c=1:1:$\sqrt{2}$.
探究:如图③,在△ABC中,AB=AC,∠A=120°,求出△ABC的三条边长之比.
应用:如图④,在四边形ABCD中,∠B=∠D=90°,∠C=120°,CD=2,BC=3,求出四边形ABCD的面积.
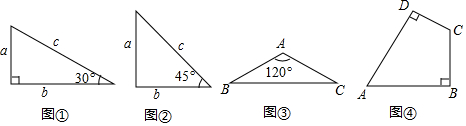
分析 在图①中,根据直角三角形中,30°的直角边是斜边的一半、勾股定理计算;
在图②中,根据等腰直角三角形的性质计算;
探究:如图③,作AD⊥BC于D,根据直角三角形中,30°的直角边是斜边的一半、勾股定理计算;
应用:如图④,延长AD、BC交于点E,根据直角三角形中,30°的直角边是斜边的一半、勾股定理计算求出边长,根据面积公式计算即可.
解答 解:在图①中,根据直角三角形的性质可知,c=2a,b=$\sqrt{3}$a,
则a:b:c=1:$\sqrt{3}$:2;
在图②中,a=b=$\frac{\sqrt{2}}{2}$c,
则a:b:c=1:1:$\sqrt{2}$,
故答案为:1:$\sqrt{3}$:2;1:1:$\sqrt{2}$;
探究:如图③,作AD⊥BC于D,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∴BD=$\frac{\sqrt{3}}{2}$AB,
∴BC=$\sqrt{3}$AB,
∴△ABC的三条边长之比1:1:$\sqrt{3}$;
应用:如图④,延长AD、BC交于点E,
∵∠B=∠D=90°,∠BCD=120°,
∴∠A=60°,
∴∠E=30°,
∴EC=2CD=4,
∴DE=2$\sqrt{3}$,BE=BC+CE=7,
∴AB=$\frac{\sqrt{3}}{3}$BE=$\frac{7\sqrt{3}}{3}$,
∴四边形ABCD的面积=S△EAB-S△EDC=$\frac{1}{2}$×$\frac{7\sqrt{3}}{3}$×7-$\frac{1}{2}$×2$\sqrt{3}×$2=$\frac{37\sqrt{3}}{6}$.
点评 本题考查的是直角三角形的性质、等腰三角形的性质、等腰直角三角形的性质,掌握相关的性质定理、灵活运用勾股定理是解题的关键.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | (-2,-5) | B. | (-1,0) | C. | (0,3) | D. | (1,5) |
| A. | y=1 | B. | y=-1 | C. | y=2 | D. | y=-2 |
| A. | (-9,-4) | B. | (-1,-2) | C. | (2,9) | D. | (5,3) |
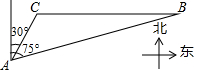 如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321) 如图,灯塔A在港口P的南偏东45°方向,距离港口20$\sqrt{2}$海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.
如图,灯塔A在港口P的南偏东45°方向,距离港口20$\sqrt{2}$海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.