题目内容
16.四边形ABCD内接于⊙O,点E为AD上一点,连接AC、CB,∠B=∠AEC.(1)如图1,求证:CE=CD;
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC=$\frac{5\sqrt{3}}{11}$,EG=2,求AE的长.
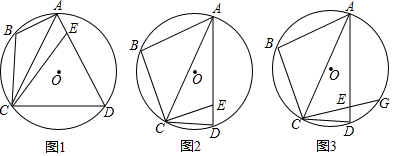
分析 (1)欲证明CE=CD,只要证明∠CED=∠D,利用等角的余角相等即可;
(2)作CH⊥DE于H.设∠ECH=α,想办法用α表示∠BAC以及∠CAE即可解决问题;
(3)连接AG,作GN⊥AC,AM⊥EG,首先证明∠CAG=∠BAC,由tan∠BAC=$\frac{5\sqrt{3}}{11}$,设NG=5$\sqrt{3}$m,可得AN=11m,AG=$\sqrt{A{N}^{2}+N{G}^{2}}$=14m,由∠ACG=60°,推出CN=5m,AM=8$\sqrt{3}$m,MG=$\sqrt{A{G}^{2}-A{M}^{2}}$=2m=1,推出m=$\frac{1}{2}$,推出CE=CD=CG-EG=10m-2=3推出AE=$\sqrt{A{M}^{2}+E{M}^{2}}$=$\sqrt{{1}^{2}+(4\sqrt{3})^{2}}$=7;
解答 (1)证明:∵四边形ABCD内接于⊙O
∴∠B+∠D=180°,
∵∠B=∠AEC,
∴∠AEC+∠D=180°,
∵∠AEC+∠CED=180°,
∴∠D=∠CED,
∴CE=CD.
(2)解:作CH⊥DE于H.
设∠ECH=α,由(1)CE=CD,
∴∠ECD=2α,
∵∠B=∠AEC,∠B+∠CAE=120°,
∴∠CAE+∠AEC=120°
∴∠ACE=180°-∠AEC-∠ACE=60°,
∴∠CAE=90°-∠ACH=90°-(60°+α)=30°-α,
∠ACD=∠ACH+∠HCD=60°+2α,
∵∠ACD=2∠BAC,
∴∠BAC=30°+α,
∴∠BAD=∠BAC+∠CAE=30°+α+30°-α=60°.
(3)连接AG,作GN⊥AC,AM⊥EG
∵∠CED=∠AEG,∠CDE=∠AGE,∠CED=∠CDE,
∴∠AEG=∠AGE,
∴AE=AG,
∴EM=MG=$\frac{1}{2}$EG=1,
∴∠EAG=∠ECD=2α,
∴∠CAG=∠CAD+∠DAG=30°-α+2α=∠BAC,
∵tan∠BAC=$\frac{5\sqrt{3}}{11}$,
∴设NG=5$\sqrt{3}$m,可得AN=11m,AG=$\sqrt{A{N}^{2}+N{G}^{2}}$=14m,
∵∠ACG=60°,
∴CN=5m,AM=8$\sqrt{3}$m,MG=$\sqrt{A{G}^{2}-A{M}^{2}}$=2m=1,
∴m=$\frac{1}{2}$,
∴CE=CD=CG-EG=10m-2=3
∴AE=$\sqrt{A{M}^{2}+E{M}^{2}}$=$\sqrt{{1}^{2}+(4\sqrt{3})^{2}}$=7.
点评 本题考查圆综合题、等腰三角形的性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考压轴题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | a+a=a2 | B. | a2•2a3=2a6 | C. | $\sqrt{6a}$÷$\sqrt{2a}$=3 | D. | (-ab3)2=a2b6 |
| A. | 若a是非负数,则a≥0 | B. | 若a不大于b,则a≤b | ||
| C. | 若a>b,则-3a>-3b | D. | 若a>b,则a-b>0 |
 如图,△ABC是等腰三角形,AB=AC=3,BC=1. 点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为( )
如图,△ABC是等腰三角形,AB=AC=3,BC=1. 点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
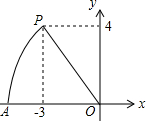 如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的坐标为(-5,0).
如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的坐标为(-5,0).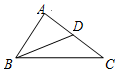 如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示). 如图,直线PC是AB的垂直平分线,垂足C,且∠A=35°,则∠B=35°.
如图,直线PC是AB的垂直平分线,垂足C,且∠A=35°,则∠B=35°. 如图,在直角三角形ABC中,斜边AB上的中线CD=AC,则∠B=30°.
如图,在直角三角形ABC中,斜边AB上的中线CD=AC,则∠B=30°.