题目内容
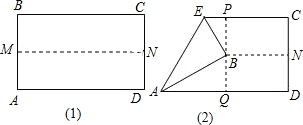
如图(1)先把一张矩形纸片ABCD上下对折,设折痕为MN;如图(2)再把点B叠在折痕线上,得到△ABE,过点B向右折纸片,使D、Q、A三点扔保持在一条直线上,得折痕PQ.
(1)求证:△PBE∽△QAB.
(2)你认为△PBE和△BAE相似吗?若相似给出证明;若不相似请说明理由.
(3)延长EB交AD于点H,请直接写出△AEH的形状为 .
(1)求证:△PBE∽△QAB.
(2)你认为△PBE和△BAE相似吗?若相似给出证明;若不相似请说明理由.
(3)延长EB交AD于点H,请直接写出△AEH的形状为

考点:相似形综合题
专题:
分析:(1)根据∠ABE=90°得∠EBP+∠ABQ=90°,证出∠ABQ=∠PEB,再根据△PBE和△QAB都是直角三角形,得出∠BPE=∠AQB=90°,即可证出△PBE∽△QAB;
(2)根据△PBE和△BAE都是直角三角形,利用(1)的结论,结合BP=BQ可证直角的两边对应成比例,从而得出△PBE和△BAE相似;
(3)根据题意先画出图形,根据ASA证出△PBE≌△QBH得出BE=BH,再根据AB⊥EH,得出AE=AH,∠EAB=∠HAB=60°,从而得出答案.
(2)根据△PBE和△BAE都是直角三角形,利用(1)的结论,结合BP=BQ可证直角的两边对应成比例,从而得出△PBE和△BAE相似;
(3)根据题意先画出图形,根据ASA证出△PBE≌△QBH得出BE=BH,再根据AB⊥EH,得出AE=AH,∠EAB=∠HAB=60°,从而得出答案.
解答:解:(1)∵∠PBE+∠ABQ=90°,∠PBE+∠PEB=90°,
∴∠ABQ=∠PEB.
在△PBE与△QAB中,
∵∠ABQ=∠PEB,∠BPE=∠AQB=90°,
∴△PBE∽△QAB.
(2)△PBE和△BAE相似.
∵△PBE∽△QAB,
∴
=
,
∵BQ=PB,
∴
=
,
又∵∠EPB=∠EBA=90°,
∴△PBE∽△BAE.
(3)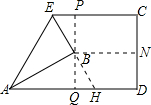 在△PBE和△QBH中,
在△PBE和△QBH中,
,
∴△PBE≌△QBH(ASA),
∴BE=BH,
∵AB⊥EH,
∴AE=AH,∠EAB=∠HAB=60°,
∴△AEH是等边三角形;
故答案为:等边三角形.
∴∠ABQ=∠PEB.
在△PBE与△QAB中,
∵∠ABQ=∠PEB,∠BPE=∠AQB=90°,
∴△PBE∽△QAB.
(2)△PBE和△BAE相似.
∵△PBE∽△QAB,
∴
| BE |
| AB |
| PE |
| BQ |
∵BQ=PB,
∴
| BE |
| AB |
| PE |
| PB |
又∵∠EPB=∠EBA=90°,
∴△PBE∽△BAE.
(3)
 在△PBE和△QBH中,
在△PBE和△QBH中,
|
∴△PBE≌△QBH(ASA),
∴BE=BH,
∵AB⊥EH,
∴AE=AH,∠EAB=∠HAB=60°,
∴△AEH是等边三角形;
故答案为:等边三角形.
点评:此题考查了相似形的综合,用到的知识点是全等三角形和相似三角形的判定与性质、等边三角形的判定,关键是画出图形,找出图形中的全等三角形和相似三角形.

练习册系列答案
相关题目
在数轴上表示整数的点称为整数点,某数轴的单位长度是1cm,若在这个数轴上随意画出一条长2015cm的线段AB,则被线段AB盖住的整数有( )
| A、2012个或2013个 |
| B、2013个或2014个 |
| C、2014个或2015个 |
| D、2015个或2016个 |
下列语句中,正确的是( )
| A、xy+1是一个一次二项式 | ||||
B、-
| ||||
| C、x2y和-yx2是同类项 | ||||
| D、-a3b2c的次数是5 |
下列说法正确的是( )
| A、绝对值大的数一定大于绝对值小的数 |
| B、任何有理数的绝对值都不可能是负数 |
| C、任何有理数的相反数都是正数 |
| D、有理数的绝对值都是正数 |
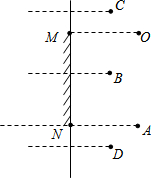 如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有
如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有