题目内容
16.国家为了鼓励青少年长才,特别是贫困家庭的孩子能上得起大学,设置了教育储蓄其优惠在于,目前暂不征收利息税,为了准备小雷5年后上大学的学费6000元,他的父母现在就参加了教育储蓄,小雷和他父母讨论了以下两种方案:(1)先存一个2年期,2年后将本息和再转存一个3年期
(2)直接存入一个5年期
你认为以上两种方案,哪种开始存入的本金较少?
分析 根据在银行存钱这一问题中所用到的公式:本息和=本金+利息×时间,分别列出两种方案的算式,根据两种所得的钱数相等,比较即可.
解答 解:设(1)的本金为a元,(2)的本金为b元,利率为m.
则(1)方案:3×2a(1+m)2=6000①,
(2)方案:5b(1+m)=6000②,
$\frac{①}{②}=\frac{6a(1+m)^{2}}{5b(1+m)}=1$
即$\frac{6a(1+m)}{5b}=1$
解得:b=a+$\frac{a+6am}{5}$,
∴b>a,
∴方案(1)存入的本金少.
点评 本题考查了一元一次方程的应用,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,然后进行对比.

练习册系列答案
相关题目
6.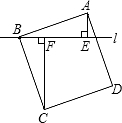 如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )
如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )
 如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )
如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{5}$ |
7.在平行四边形ABCD中,AC=10,BD=6,则边长AB,AD的可能取值为( )
| A. | AB=4,AD=4 | B. | AB=4,AD=7 | C. | AB=9,AD=2 | D. | AB=6,AD=2 |
11.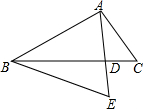 如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:4,AE=7,BD=$\frac{10}{3}$,则DC的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:4,AE=7,BD=$\frac{10}{3}$,则DC的长等于( )
 如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:4,AE=7,BD=$\frac{10}{3}$,则DC的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:4,AE=7,BD=$\frac{10}{3}$,则DC的长等于( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{18}{5}$ |
1.化简$\sqrt{{{(-8)}^2}}$的结果是( )
| A. | -8 | B. | 8 | C. | ±4 | D. | ±8 |
 如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点.
如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点. 一个印有“我喜欢数学课”字样的立方体纸盒表面展开图如图所示,则与印有“欢”字相对的表面上印有我字.
一个印有“我喜欢数学课”字样的立方体纸盒表面展开图如图所示,则与印有“欢”字相对的表面上印有我字.