题目内容
11.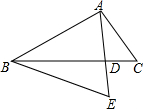 如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:4,AE=7,BD=$\frac{10}{3}$,则DC的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:4,AE=7,BD=$\frac{10}{3}$,则DC的长等于( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{18}{5}$ |
分析 根据相似三角形的判定与性质,可得$\frac{DC}{DE}$=$\frac{AD}{BD}$,再根据AD:DE=3:4,AE=7,可得AD、DE的长,根据比例的性质,可得答案.
解答 解:∵∠C=∠E,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴$\frac{DC}{DE}$=$\frac{AD}{BD}$,
又∵AD:DE=3:4,AE=7,
∴AD=3,DE=4,
∵BD=$\frac{10}{3}$,
∴$\frac{DC}{DE}$=$\frac{AD}{BD}$,即$\frac{CD}{4}$=$\frac{3}{\frac{10}{3}}$.
∴DC=$\frac{18}{5}$,
故选D.
点评 本题考查了相似三角形的判定与性质,比例的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
19. 观察图,在下列四种图形变换中,该图案不包含的变换是( )
观察图,在下列四种图形变换中,该图案不包含的变换是( )
 观察图,在下列四种图形变换中,该图案不包含的变换是( )
观察图,在下列四种图形变换中,该图案不包含的变换是( )| A. | 旋转 | B. | 轴对称 | C. | 位似 | D. | 平移 |
3.与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{20}$ |
20.如果∠1和∠2是同旁内角,且∠1=30°,那么∠2为( )
| A. | 30° | B. | 60° | C. | 150° | D. | 不能确定 |
 在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3),B(3,1),O(0,0).
在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3),B(3,1),O(0,0).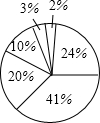 根据如图的数据制作扇形统计图并回答问题
根据如图的数据制作扇形统计图并回答问题